题目内容
已知:关于x的方程x2-2(m+1)x+m2=0
(1)当m取什么值时,原方程没有实数根;
(2)对m选取一个你喜欢的非零整数,使原方程有两个实数根,并求这两个实数根.
(1)当m取什么值时,原方程没有实数根;
(2)对m选取一个你喜欢的非零整数,使原方程有两个实数根,并求这两个实数根.
考点:根的判别式
专题:
分析:(1)要使原方程没有实数根,只需△<0即可,然后可以得到关于m的不等式,由此即可求出m的取值范围;
(2)根据(1)中求得的范围,在范围之外确定一个m的值,再利用公式法求解即可.
(2)根据(1)中求得的范围,在范围之外确定一个m的值,再利用公式法求解即可.
解答:解:(1)∵方程没有实数根,
∴b2-4ac=[-2(m+1)]2-4m2=8m+4<0,
∴m<-
,
∴当m<-
时,原方程没有实数根;
(2)由(1)可知,当m≥-
时,方程有实数根,
当m=1时,原方程变为x2-4x+1=0,
设此时方程的两根分别为x1,x2,
解得x1=2+
,x2=2-
.
∴b2-4ac=[-2(m+1)]2-4m2=8m+4<0,
∴m<-
| 1 |
| 2 |
∴当m<-
| 1 |
| 2 |
(2)由(1)可知,当m≥-
| 1 |
| 2 |
当m=1时,原方程变为x2-4x+1=0,
设此时方程的两根分别为x1,x2,
解得x1=2+
| 3 |
| 3 |
点评:本题考查了一元二次方程根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
同时考查了一元二次方程的解法.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
同时考查了一元二次方程的解法.

练习册系列答案
相关题目
 如图,在正方形网格上有相似三角形△A1B1C1和△A2B2C2,则△A1B1C1和△A2B2C2的面积比为( )
如图,在正方形网格上有相似三角形△A1B1C1和△A2B2C2,则△A1B1C1和△A2B2C2的面积比为( )| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
下列命题中错误的是( )
| A、平分弦的直径垂直于弦 |
| B、三角形的外心到三角形各顶点的距离相等 |
| C、同圆或等圆中,相等的圆心角所对的弧相等 |
| D、经过切点垂直于切线的直线必经过圆心 |
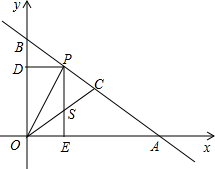 如图,一次函数y=-
如图,一次函数y=-