题目内容
14. 如图,若点P的坐标为(-2,2),过点P的一条直线交抛物线y=x2于A、B两点,当PA=AB时,点A的坐标是(-1,1)或(-3,9).
如图,若点P的坐标为(-2,2),过点P的一条直线交抛物线y=x2于A、B两点,当PA=AB时,点A的坐标是(-1,1)或(-3,9).
分析 设A(m,m2),分别过点P、A、B作x轴垂线,垂足分别为点G、E、F,用m表示出OF和BF的长,根据点B在抛物线y=x2上,即可求出点A的坐标.
解答 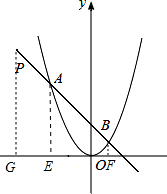 解:设A(m,m2),
解:设A(m,m2),
如图所示,分别过点P、A、B作x轴垂线,垂足分别为点G、E、F.
∵PA=AB,
∴AE是梯形PGFB的中位线,
∴GE=EF,AE=$\frac{1}{2}$(PG+BF).
∵OF=|EF-OE|,GE=EF,
∴OF=|GE-EO|,
∵GE=GO-EO=2+m,EO=-m,
∴OF=|2+m-(-m)|=|2+2m|,
∴OF=2m+2,
∵AE=$\frac{1}{2}$(PG+BF),
∴BF=2AE-PG=2m2-2,
∴B(2+2m,2m2-2).
∵点B在抛物线y=x2上,
∴2m2-2=(2+2m)2
解得:m=1或-3,
当m=-1时,m2=1;当m=-3时,m2=9,
点A的坐标为(-1,1)或(-3,9).
故答案为(-1,1)或(-3,9).
点评 本题主要考查了二次函数的性质,解答本题的关键是正确地作出辅助线,求出点B的坐标,此题有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.据淮安日报报道,2013年5月28日淮安最高气温是27℃,最低气温是20℃,则当天淮安气温t(℃)的变化范围是( )
| A. | t>27 | B. | t≤20 | C. | 20<t<27 | D. | 20≤t≤27 |
5.观察下面一列有序数对:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),
(2,3),(3,2),(4,1),(1,5),(2,4),…,按这些规律,第50个有序数对是( )
(2,3),(3,2),(4,1),(1,5),(2,4),…,按这些规律,第50个有序数对是( )
| A. | (3,8) | B. | (4,7) | C. | (5,6) | D. | (6,5) |
2.已知正方形的边长为a厘米,如果它的一边长增加3厘米,另一边减少3厘米,那么它的面积( )
| A. | 不变 | B. | 减少9平方厘米 | C. | 增加9平方厘米 | D. | 不能确定 |