题目内容
10.阅读材料,回答问题:(1+$\frac{1}{2}$)×(1-$\frac{1}{3}$)=$\frac{3}{2}$×$\frac{2}{3}$=1;
(1+$\frac{1}{2}$)×(1+$\frac{1}{4}$)×(1-$\frac{1}{3}$)×(1-$\frac{1}{5}$)=$\frac{3}{2}$×$\frac{5}{4}$×$\frac{2}{3}$×$\frac{4}{5}$=1×1=1.
根据以上信息,请求出下式的结果:
(1+$\frac{1}{2}$)×(1+$\frac{1}{4}$)×(1+$\frac{1}{6}$)×…×(1+$\frac{1}{20}$)×(1-$\frac{1}{3}$)×(1-$\frac{1}{5}$)×(1-$\frac{1}{7}$)×…×(1-$\frac{1}{21}$).
分析 根据有理数的加法,可得分数的乘法,再根据乘法交换律和结合律可得结果.
解答 解:原式=$\frac{3}{2}$×$\frac{5}{4}$×$\frac{7}{6}$×…×$\frac{21}{20}$×$\frac{2}{3}$×$\frac{4}{5}$×$\frac{6}{7}$×…×$\frac{20}{21}$
=($\frac{3}{2}$×$\frac{2}{3}$)×($\frac{5}{4}$×$\frac{4}{5}$)×($\frac{7}{6}$×$\frac{6}{7}$)×…×($\frac{21}{20}$×$\frac{20}{21}$)
=1×1×1×…×1
=1.
点评 本题考查了规律型,发现规律:互为倒数的因数成对出现,利用结合律是解题关键.

练习册系列答案
相关题目
5.相反数等于其本身的数有( )
| A. | 1个 | B. | 2个 | C. | 0个 | D. | 无数个 |
17.下列计算中,正确的是( )
| A. | x3•x3=x6 | B. | x3+x3=x6 | C. | (x3)2=x9 | D. | x6÷x2=x3 |
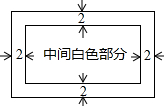 如图,小红用一张周长为88cm的长方形白纸做一张贺卡,长方形白纸内部的四周涂上宽为2cm的彩色花边.
如图,小红用一张周长为88cm的长方形白纸做一张贺卡,长方形白纸内部的四周涂上宽为2cm的彩色花边.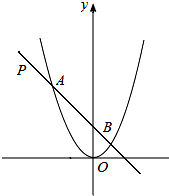 如图,若点P的坐标为(-2,2),过点P的一条直线交抛物线y=x2于A、B两点,当PA=AB时,点A的坐标是(-1,1)或(-3,9).
如图,若点P的坐标为(-2,2),过点P的一条直线交抛物线y=x2于A、B两点,当PA=AB时,点A的坐标是(-1,1)或(-3,9).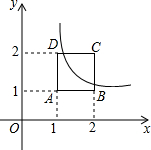 如图,反比例函数y=$\frac{k}{x}$的图象与正方形ABCD在BC和CD边上相交.已知A(1,1),C(2,2),则k的值可能是( )
如图,反比例函数y=$\frac{k}{x}$的图象与正方形ABCD在BC和CD边上相交.已知A(1,1),C(2,2),则k的值可能是( )