Question

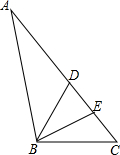
如图，在△ABD和△ACE中，AB=AD，AC=AE，AC∥BD，AD∥EC，∠ACE=70°．
（1）求∠BAD的度数；
（2）求证：BC=DE．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：（1）根据平行线求出∠ADB=∠CE=70°，求出∠ABD=70°，根据三角形内角和定理求出即可；
（2）求出∠EAC=∠DAB，推出∠EAD=∠CAB，根据SAS推出△EAD≌△CAB即可．

解答：（1）解：∵AC∥BD，AD∥EC，∠ACE=70°，
∴∠CAD=∠ACE=70°，
∴∠ADB=∠CAD=70°，
∵AB=AD，
∴∠ABD=∠ADB=70°，
∴∠BAD=180°-70°-70°=40°；

（2）证明：∵AC=AE，∠ACE=70°，
∴∠AEC=∠ACE=70°，
∴∠EAC=180°-70°-70°=40°，
∵∠BAD=40°，
∴∠EAC=∠BAD，
∴∠EAC+∠CAD=∠BAD+∠CAD，
∴∠EAD=∠CAB，
在△EAD和△CAB中，

AE=AC ∠EAD=∠CAB AD=AB

，
∴△EAD≌△CAB（SAS），
∴BC=DE．

点评：本题考查了全等三角形的性质和判定，三角形内角和定理，等腰三角形的性质的应用，注意：全等三角形的对应边相等，对应角相等．