题目内容
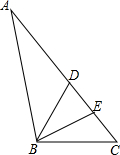 已知在△ABC中,D是边AC上的一点,∠CBD的角平分线交AC于点E,且AE=AB,求证:AE2=AD•AC.
已知在△ABC中,D是边AC上的一点,∠CBD的角平分线交AC于点E,且AE=AB,求证:AE2=AD•AC.考点:相似三角形的判定与性质
专题:证明题
分析:根据角平分线的性质和外角等于不相邻两内角和即可求得∠ABD=∠C,可证明△ABD∽△ABC,即可解题.
解答:证明:∵BE平分∠CBD,
∴∠DBE=∠CBE,
∵AE=AB,
∴∠ABE=∠AEB,
∵∠ABE=∠ABD+∠DBE,∠AEB=∠C+∠CBE,
∴∠ABD=∠C,
∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ABC,
∴AB:AD=AC:AB,即:AB•AB=AD•AC,
∵AE=AB,
∴AE•AE=AD•AC.
∴∠DBE=∠CBE,
∵AE=AB,
∴∠ABE=∠AEB,
∵∠ABE=∠ABD+∠DBE,∠AEB=∠C+∠CBE,
∴∠ABD=∠C,
∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ABC,
∴AB:AD=AC:AB,即:AB•AB=AD•AC,
∵AE=AB,
∴AE•AE=AD•AC.
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
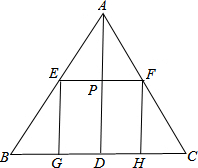 △ABC中,已知BC=6,点D是BC边上的中点,AD=5,点P为线段AD上一点(与A、D不重合),过P作EF∥BC分别交AB,AC于点E、F,过E、F分别作EG∥AD,FH∥AD交BC边于点G.
△ABC中,已知BC=6,点D是BC边上的中点,AD=5,点P为线段AD上一点(与A、D不重合),过P作EF∥BC分别交AB,AC于点E、F,过E、F分别作EG∥AD,FH∥AD交BC边于点G. 如图,在边长为1个单位长度的小正方形组成的网格中,按要求作图.
如图,在边长为1个单位长度的小正方形组成的网格中,按要求作图. 如图,在△ABD和△ACE中,AB=AD,AC=AE,AC∥BD,AD∥EC,∠ACE=70°.
如图,在△ABD和△ACE中,AB=AD,AC=AE,AC∥BD,AD∥EC,∠ACE=70°.