题目内容
6.若抛物线y=-x2经过适当的平移后经过点(-1,0)和(2,3),求平移后抛物线的解析式.分析 根据函数图象平移不改变图象的形状,可得二次项的系数不变,根据待定系数法,可得函数解析式.
解答 解:设平移后的解析式为y=-x2+bx+c,
由抛物线y=-x2经过适当的平移后经过点(-1,0)和(2,3),得
$\left\{\begin{array}{l}{-1-b+c=0}\\{-4+2b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=0}\\{c=1}\end{array}\right.$.
故平移后抛物线的解析式y=-x2+1.
点评 本题考查了二次函数图象与几何变换,利用函数图象平移不改变图象的形状得出二次项的系数不变是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.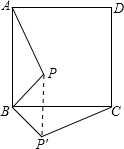 正方形ABCD内一点P,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP′,则PP′的长为( )
正方形ABCD内一点P,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP′,则PP′的长为( )
 正方形ABCD内一点P,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP′,则PP′的长为( )
正方形ABCD内一点P,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP′,则PP′的长为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{2}$ |
18.已知y1=x+1,y2=3x-5.当y1>y2时,x的取值范围是( )
| A. | x>3 | B. | x<3 | C. | x<-3 | D. | x>-3 |
 如图,BD是△ABC的角平分线,∠A=40°,∠ABC=70°,DF⊥BC于F,E为BC延长线上一点,CE=CD,求证:BF=EF.
如图,BD是△ABC的角平分线,∠A=40°,∠ABC=70°,DF⊥BC于F,E为BC延长线上一点,CE=CD,求证:BF=EF.