题目内容
17.下列运算,结果正确的是( )| A. | m2+m2=m4 | B. | (m+$\frac{1}{m}$)2=m2+$\frac{1}{{m}^{2}}$ | C. | (3mn2)2=6m2n4 | D. | 2m2n÷$\frac{m}{n}$=2mn2 |
分析 A:根据整式的混合运算方法计算即可.
B:根据完全平方公式的计算方法判断即可.
C:根据积的乘方的运算方法计算即可.
D:根据分式的混合运算方法计算即可.
解答 解:∵m2+m2=2m2,
∴选项A错误;
∵(m+$\frac{1}{m}$)2=m2+$\frac{1}{{m}^{2}}$+2,
∴选项B错误;
∵(3mn2)2=9m2n4,
∴选项C错误;
∵2m2n÷$\frac{m}{n}$=2mn2,
∴选项D正确.
故选:D.
点评 (1)此题主要考查了分式的混合运算,要注意运算顺序,分式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.
(2)此题还考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.
(3)此题还考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
7.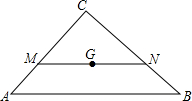 已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )
已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )
 已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )
已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )| A. | 3 | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
5. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
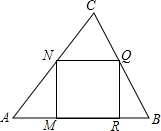 如图,已知正方形MNQR内接于锐角△ABC中,设△ABC的面积为S,正方形MNQR的面积为S1,求证:S1≤$\frac{1}{2}$S.
如图,已知正方形MNQR内接于锐角△ABC中,设△ABC的面积为S,正方形MNQR的面积为S1,求证:S1≤$\frac{1}{2}$S.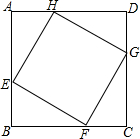 如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
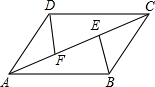 如图,在?ABCD中,E、F为对角线AC上两点,且BE∥DF,请从图中找出一对全等三角形:△ADF≌△BEC.
如图,在?ABCD中,E、F为对角线AC上两点,且BE∥DF,请从图中找出一对全等三角形:△ADF≌△BEC.