题目内容
2.在梯形ABCD中,AB∥CD,AC平分∠BAD,AC⊥BC,BC=2,AB=4,则梯形ABCD的周长为10.分析 作CE∥AD交AB于E,则四边形AECD是平行四边形,∠CEB=∠BAD,得出AD=CE,证出AD=CD,再证明∠1=30°,证出∠B=∠CEB=60°,得出CE=BC=2,AD=CD=2,即可得出结果.
解答 解:作CE∥AD交AB于E,如图所示: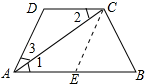
则四边形AECD是平行四边形,∠CEB=∠BAD,
∴AD=CE,
∵AB∥CD,
∴∠1=∠2,
∵AC平分∠BAD,
∴∠1=∠3,
∴∠2=∠3,
∴AD=CD,
∵AC⊥BC,BC=2,AB=4,
∴∠1=30°,
∴∠3=30°,∠B=90°-30°=60°,
∴∠CEB=∠BAD=30°+30°=60°,
∴∠B=∠CEB=60°,
∴CE=BC=2,
∴AD=CD=2,
∴梯形ABCD的周长=AB+BC+CD+AD=4+2+2+2=10.
故答案为:10.
点评 本题考查了梯形的性质、平行四边形的判定与性质、等腰三角形的判定;熟练掌握梯形的性质,通过作辅助线证出三角形是等腰三角形是解决问题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
10.下列四个结论中,错误的有( )
(1)负数没有立方根;
(2)一个数的立方根不是正数就是负数;
(3)一个正数的平方根一定是它的算术平方根;
(4)一个数的平方根一定有两个.
(1)负数没有立方根;
(2)一个数的立方根不是正数就是负数;
(3)一个正数的平方根一定是它的算术平方根;
(4)一个数的平方根一定有两个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4 个 |
7.下列命题正确的是( )
| A. | 一组对边相等,另一组对边平行的四边形一定是平行四边形 | |
| B. | 对角线相等的四边形一定是矩形 | |
| C. | 两条对角线互相垂直的四边形一定是正方形 | |
| D. | 两条对角线相等且互相垂直平分的四边形一定是正方形 |
 如图,△AEB和△FEC是否相似?为什么?
如图,△AEB和△FEC是否相似?为什么?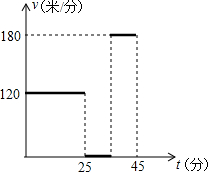 某兴趣小组从学校出发骑车去植物园参观,先经过一段上坡路后到达途中一处景点,停车10分钟进行参观,然后又经一段下坡路到达植物园,行程情况如图,若他们上、下坡路速度不变,则这个兴趣小组的同学按原路返回所用的时间为$\frac{95}{3}$分钟(途中不停留)
某兴趣小组从学校出发骑车去植物园参观,先经过一段上坡路后到达途中一处景点,停车10分钟进行参观,然后又经一段下坡路到达植物园,行程情况如图,若他们上、下坡路速度不变,则这个兴趣小组的同学按原路返回所用的时间为$\frac{95}{3}$分钟(途中不停留)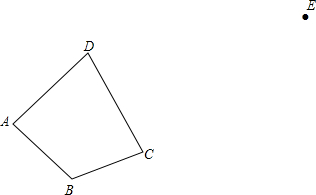 如图,四边形ABCD中:
如图,四边形ABCD中: 如图,AB=CD,BD=AC,AB∥CD,求证:AB⊥BC.
如图,AB=CD,BD=AC,AB∥CD,求证:AB⊥BC. (1)四边形不具有稳定性,要使四边形木架不变形,至少要再钉上1根木条.
(1)四边形不具有稳定性,要使四边形木架不变形,至少要再钉上1根木条.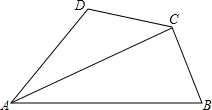 已知,四边形ABCD中,∠D与∠B互补,且对角线AC平分∠BAD,请比较BC与DC的大小,并证明你的结论.
已知,四边形ABCD中,∠D与∠B互补,且对角线AC平分∠BAD,请比较BC与DC的大小,并证明你的结论.