题目内容
 如图,P为弦AB上一点,CP⊥OP交⊙O于点C,AB=8,
如图,P为弦AB上一点,CP⊥OP交⊙O于点C,AB=8,| AP |
| PB |
| 1 |
| 3 |
考点:相交弦定理,垂径定理
专题:
分析:延长CP交⊙O于D.由垂径定理可知CP=DP,由AB=8,
=
,得到AP=
AB=2,PB=
AB=6.再根据相交弦定理得出PC•PD=AP•PB,代入数值计算即可求解.
| AP |
| PB |
| 1 |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
解答: 解:如图,延长CP交⊙O于D.
解:如图,延长CP交⊙O于D.
∵CP⊥OP,
∴CP=DP.
∵AB=8,
=
,
∴AP=
AB=2,PB=
AB=6.
∵AB、CD是⊙O的两条相交弦,交点为P,
∴PC•PD=AP•PB,
∴PC2=2×6,
∴PC=2
.
 解:如图,延长CP交⊙O于D.
解:如图,延长CP交⊙O于D.∵CP⊥OP,
∴CP=DP.
∵AB=8,
| AP |
| PB |
| 1 |
| 3 |
∴AP=
| 1 |
| 4 |
| 3 |
| 4 |
∵AB、CD是⊙O的两条相交弦,交点为P,
∴PC•PD=AP•PB,
∴PC2=2×6,
∴PC=2
| 3 |
点评:本题考查了相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.同时考查了垂径定理,准确作出辅助线是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
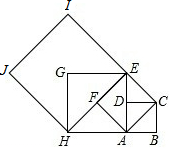 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a2=
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a2=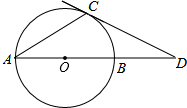 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠A的度数.
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠A的度数.