题目内容
14．已知正比例函数y=kx（k＞0）的图象上有两点A（x1，y1）、B（x2，y2），且x1＞x2，则y1与 y2的大小关系是（ ）| A． | y1＜y2 | B． | y1＞y2 | C． | y1=y2 | D． | 不能确定 |
分析 先根据正比例函数的系数k判断出函数的增减性，再由x1＞x2即可得出结论．
解答 解：∵正比例函数y=kx中，k＞0，
∴此函数是增函数．
∵x1＞x2，
∴y1＞y2．
故选B．
点评 本题考查的是一次函数图象上点的坐标特点，熟知一次函数的增减性与系数k的关系是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，∠A=∠D=90°，CD平分∠ACB，AB与CD相交于点E．
9．
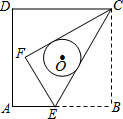如图，正方形ABCD的边长为9，点E是AB上的一点，将△BCE沿CE折叠至△FCE，若CF，CE恰好与以正方形ABCD的中心为圆心的⊙O相切，则折痕CE的长为（ ）
如图，正方形ABCD的边长为9，点E是AB上的一点，将△BCE沿CE折叠至△FCE，若CF，CE恰好与以正方形ABCD的中心为圆心的⊙O相切，则折痕CE的长为（ ）| A． | 4$\sqrt{3}$ | B． | $\frac{8}{3}$$\sqrt{3}$ | C． | 4$\sqrt{5}$ | D． | 6$\sqrt{3}$ |