题目内容
 如图,△ABC中,∠A=90°,点D、E分别在AC和AB上,试说明BD2-DE2=BC2-CE2.
如图,△ABC中,∠A=90°,点D、E分别在AC和AB上,试说明BD2-DE2=BC2-CE2.考点:勾股定理
专题:证明题
分析:在直角三角形ABD与直角三角形ACE中,利用勾股定理列出关系式,表示出BD2+CE2,在直角三角形ABC与直角三角形AED中,利用勾股定理列出关系式,表示出BC2+ED2,整理即可得证.
解答:
证明:在Rt△ABD和Rt△ACE中,
根据勾股定理得:BD2=AB2+AD2,CE2=AE2+AC2,
∴BD2+CE2=AB2+AD2+AE2+AC2,
在Rt△ABC和Rt△AED中,
根据勾股定理得:BC2=AB2+AC2,ED2=AD2+AE2,
∴BC2+ED2=AB2+AC2+AD2+AE2,
∴BD2+CE2=BC2+ED2,
则BD2-DE2=BC2-CE2.
根据勾股定理得:BD2=AB2+AD2,CE2=AE2+AC2,
∴BD2+CE2=AB2+AD2+AE2+AC2,
在Rt△ABC和Rt△AED中,
根据勾股定理得:BC2=AB2+AC2,ED2=AD2+AE2,
∴BC2+ED2=AB2+AC2+AD2+AE2,
∴BD2+CE2=BC2+ED2,
则BD2-DE2=BC2-CE2.
点评:此题考查了勾股定理,勾股定理为直角三角形中,两直角边的平方等于斜边的平方,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在直角坐标系中,一直线l向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B(-
,0),则直线l的函数关系式为( )
| 3 |
A、y=-
| ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=-
|
如图1,圆的周长为4个单位.在该圆的4等分点处分别标上字母m、n、p、q.如图2,先将圆周上表示p的点与数轴原点重合,然后将该圆沿着数轴的负方向滚动,则数轴上表示-2013的点与圆周上重合的点对应的字母是( )


| A、m | B、n | C、p | D、q |
两个多边形相似的条件是( )
| A、对应角相等 |
| B、对应边成比例 |
| C、对应角相等或对应边成比例 |
| D、对应角相等且对应边成比例 |
如图所示,全等的三角形是( )


| A、Ⅰ和Ⅱ | B、Ⅱ和Ⅳ |
| C、Ⅱ和Ⅲ | D、Ⅰ和Ⅲ |
当a<0时,下列四个结论:①a2>0;②a2=(-a)2 ;③-a3=|a3|=4;④-a2=|-a2|,其中一定正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
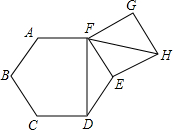 如图,在正六边形ABCDEF的外侧,作正方形EFGH,则∠DFH的度数为
如图,在正六边形ABCDEF的外侧,作正方形EFGH,则∠DFH的度数为 如图,∠AOB=110°,则∠ACB=
如图,∠AOB=110°,则∠ACB=