题目内容
8. 如图,AB是⊙0的直径,C、D是半圆的三等分点,则∠C+∠E+∠D=120°.
如图,AB是⊙0的直径,C、D是半圆的三等分点,则∠C+∠E+∠D=120°.
分析 由于$\widehat{AE}$+$\widehat{BE}$是一个半圆,故∠C+∠D=$\frac{1}{2}$×180°=90°,再根据C、D是半圆的三等分点可知$\widehat{CD}$=$\frac{1}{3}$×180°=60°,故∠E=$\frac{1}{2}$$\widehat{CD}$=$\frac{1}{2}$×60°=30°,故可求出答案.
解答 解:∵AB是⊙0的直径,C、D是半圆的三等分点
解:∵$\widehat{AE}$+$\widehat{BE}$是一个半圆,
∴∠C+∠D=$\frac{1}{2}$×180°=90°,
∵据C、D是半圆的三等分点,
∴$\widehat{CD}$=$\frac{1}{3}$×180°=60°,
∴∠E=$\frac{1}{2}$$\widehat{CD}$=$\frac{1}{2}$×60°=30°,
∴∠C+∠D+∠E=90°+30°=120°.
故答案为:120°.
点评 本题考查的是圆周角定理及圆心角、弧、弦的关系,解答此题时要熟知弧的度数等于此弧所对圆心角的度数.

练习册系列答案
相关题目
18.方程2x2+x-1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 只有一个实数根 |
17.在函数$y=\frac{{\sqrt{x+1}}}{2x-1}$中,自变量x的取值范围是( )
| A. | x≥-1 | B. | x>-1且x≠$\frac{1}{2}$ | C. | x≥-1且x≠$\frac{1}{2}$ | D. | x≥-1 |
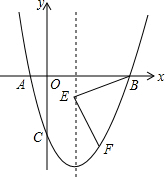 如图所示,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,E为x轴下方的对称轴上一点且EF⊥BE交抛物线于F,且EB=EF,求点F坐标.
如图所示,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,E为x轴下方的对称轴上一点且EF⊥BE交抛物线于F,且EB=EF,求点F坐标.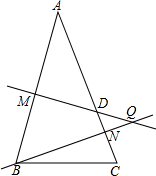 如图,在△ABC中,△ABC中,∠ABC=∠C,AB的垂直平分线MQ交AC于D,CD的垂直平分线恰好过点B,求∠A的度数.
如图,在△ABC中,△ABC中,∠ABC=∠C,AB的垂直平分线MQ交AC于D,CD的垂直平分线恰好过点B,求∠A的度数.