题目内容
因式分解:3x2+4xy-y2.
考点:因式分解
专题:
分析:首先提取公因式3,再利用配方法把式子变形为3[(x2+2×
xy+
y2)-
y2-
y2],然后利用完全平方公式进行分解,再利用平方差公式进行三次分解即可.
| 2 |
| 3 |
| 4 |
| 9 |
| 1 |
| 3 |
| 4 |
| 9 |
解答:解:3x2+4xy-y2
=3(x2+
xy-
y2)
=3[(x2+2×
xy+
y2)-
y2-
y2]
=3[(x+
y)2-
y2]
=3(x+
y+
y)(x+
y-
y)
=3[x+
y)(x-
y).
=3(x2+
| 4 |
| 3 |
| 1 |
| 3 |
=3[(x2+2×
| 2 |
| 3 |
| 4 |
| 9 |
| 1 |
| 3 |
| 4 |
| 9 |
=3[(x+
| 2 |
| 3 |
| 7 |
| 9 |
=3(x+
| 2 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
| ||
| 3 |
=3[x+
2+
| ||
| 3 |
2-
| ||
| 3 |
点评:此题主要考查了因式分解,关键是掌握分解因式的方法,先提公因式,后用公式法.

练习册系列答案
相关题目
在同一直角坐标系中,抛物线y=x2+4x+5与直线y=3x的交点个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
 已知平面直角坐标系xOy(如图),直线y=x+b经过第一、三、四象限,与y轴交于点B,点A(2,t)在这条直线上,连接AO,△AOB的面积等于1,反比例函数y=
已知平面直角坐标系xOy(如图),直线y=x+b经过第一、三、四象限,与y轴交于点B,点A(2,t)在这条直线上,连接AO,△AOB的面积等于1,反比例函数y=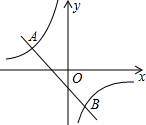 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=