Question

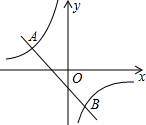如图，一次函数y=kx+b的图象与反比例函数y=

m

x

图象交于A（-2，1），B（1，n）两点．
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出当1＜x＜4时，反比例函数y的取值范围．

Answer 1

考点：反比例函数与一次函数的交点问题

专题：计算题

分析：（1）先把A点坐标代入入y=

m

x

求出m得到反比例函数解析式为y=-

2

x

，再利用反比例函数解析式确定B点坐标，然后利用待定系数法求一次函数解析式；
（2）分别计算自变量为1和4的反比例函数的函数值，然后根据反比例函数的性质确定y的取值范围．

解答：解：（1）把A（-2，1）代入y=

m

x

得m=-2×1=-2，
所以反比例函数解析式为y=-

2

x

；
把B（1，n）代入y=-

2

x

得n=-2，则B点坐标为（1，-2），
把A（-2，1），B（1，-2）代入y=kx+b得

-2k+b=1 k+b=-2

，解得

k=-1 b=-1

，
所以一次函数解析式为y=-x-1；
（2）当x=1时，y=-

2

x

=-2；当x=4时，y=-

2

x

=-

1

2

，
所以当1＜x＜4时，反比例函数y的取值范围为-2＜y＜-

1

2

．

点评：本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．也考查了待定系数法求一次函数解析式．