题目内容
9. 如图,正三角形ABC的边长为2,分别以A、B、C为圆心,1为半径画弧,与△ABC的内切圆O围成的图形为图中阴影部分,求S阴影.
如图,正三角形ABC的边长为2,分别以A、B、C为圆心,1为半径画弧,与△ABC的内切圆O围成的图形为图中阴影部分,求S阴影.
分析 直接利用等边三角形的性质结合扇形面积求法得出扇形中间空白面积,进而得出答案.
解答  解:连接AO,EO,
解:连接AO,EO,
由题意可得:AE=1,∠OAE=30°,
则tan30°=$\frac{EO}{AE}$=$\frac{EO}{1}$=$\frac{\sqrt{3}}{3}$,
故EO=$\frac{\sqrt{3}}{3}$,
则S△AEO=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{6}$,
∴S△ABC=$\frac{\sqrt{3}}{6}$×6=$\sqrt{3}$,
∴扇形中间空白面积为:S△ABC-33扇形ADE=$\sqrt{3}$-3×$\frac{60×π×{1}^{2}}{360}$=$\sqrt{3}$-$\frac{π}{4}$,
∴S阴影=π×($\frac{\sqrt{3}}{3}$)2-($\sqrt{3}$-$\frac{π}{4}$)=$\frac{7π}{12}$-$\sqrt{3}$.
点评 此题主要考查了等边三角形的性质以及扇形面积求法和三角形的内心,正确得出空白面积是解题关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
19.由于夏季电力供应紧张,某地决定对工厂实行鼓励错峰用电,规定:在每天的7:00至24:00为用电高峰期,电价为a元/度;每天00:00至7:00为用电平稳期,电价为0.2元/度,下表为某厂7、8月份的用电量和电费的情况统计表:
(1)若7月份在平稳期的用电量占当月总用电量的$\frac{1}{3}$,求a的值;
(2)若a=0.6,则8月份在平稳期的用电量占当月总用电量的多少?
| 月份 | 总用电量(万度) | 电费(万元) |
| 7 | 12 | 6.4 |
| 8 | 16 | 8.8 |
(2)若a=0.6,则8月份在平稳期的用电量占当月总用电量的多少?
17.两个相似三角形的最短边分别是5cm和3cm,它们的周长之差为12cm,那么小三角形的周长为( )
| A. | 14cm | B. | 16cm | C. | 18cm | D. | 30cm |
4. 如图,若图形A经过平移可以与图形B、C拼成一个长方形,则可能的平移方式是( )
如图,若图形A经过平移可以与图形B、C拼成一个长方形,则可能的平移方式是( )
 如图,若图形A经过平移可以与图形B、C拼成一个长方形,则可能的平移方式是( )
如图,若图形A经过平移可以与图形B、C拼成一个长方形,则可能的平移方式是( )| A. | 向右平移4格,再向下平移5格 | B. | 向右平移6格,再向下平移5格 | ||
| C. | 向右平移4格,再向下平移2格 | D. | 向右平移6格,再向下平移2格 |
1.一次函数y1=5(x+2)与y2=-2x+10,当y1≤y2时,x的取值为( )
| A. | x≤0 | B. | x≥0 | C. | x为任何实数 | D. | 以上答案都不对 |
18.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
要从中选择一名发挥稳定的运动员去参加比赛,应该选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 183 | 183 | 183 | 183 |
| 方差 | 3.6 | 5.4 | 7.2 | 8.5 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
19.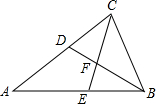 如图,△ABC中,AB=AC,BD、CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )
如图,△ABC中,AB=AC,BD、CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )
 如图,△ABC中,AB=AC,BD、CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )
如图,△ABC中,AB=AC,BD、CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
 如图,已知BEFG是长方形,A为EB延长线上一点,AF交BG于点C,D为AC上一点,且AD=BD=BF,若∠BFG=60°,则∠AFG的度数为20°.
如图,已知BEFG是长方形,A为EB延长线上一点,AF交BG于点C,D为AC上一点,且AD=BD=BF,若∠BFG=60°,则∠AFG的度数为20°.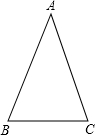 如图△ABC中,AB=AC=6,BC=4,∠A=40°.
如图△ABC中,AB=AC=6,BC=4,∠A=40°.