题目内容
19.由于夏季电力供应紧张,某地决定对工厂实行鼓励错峰用电,规定:在每天的7:00至24:00为用电高峰期,电价为a元/度;每天00:00至7:00为用电平稳期,电价为0.2元/度,下表为某厂7、8月份的用电量和电费的情况统计表:| 月份 | 总用电量(万度) | 电费(万元) |
| 7 | 12 | 6.4 |
| 8 | 16 | 8.8 |
(2)若a=0.6,则8月份在平稳期的用电量占当月总用电量的多少?
分析 (1)根据总电费=用电平稳期电费+用电高峰期电费即可得出关于a的一元一次方程,解之即可得出a值;
(2)设8月份在平稳期的用电量占当月总用电量的x,根据总电费=用电平稳期电费+用电高峰期电费即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)根据题意得:12×$\frac{1}{3}$×0.2+12×(1-$\frac{1}{3}$)a=6.4,
解得:a=0.7.
答:a的值为0.7.
(2)设8月份在平稳期的用电量占当月总用电量的x,
根据题意得:0.2×16x+0.6×16(1-x)=8.8,
解得:x=$\frac{1}{8}$.
答:8月份在平稳期的用电量占当月总用电量的$\frac{1}{8}$.
点评 本题考查了一元一次方程的应用,根据数量关系总电费=用电平稳期电费+用电高峰期电费列出一元一次方程是解题的关键.

练习册系列答案
相关题目
7.如图,在左边托盘A(固定)中放置一个重物,在右边托盘B(可左右移动)中放置一定质量的砝码,可使得仪器左右平衡,改变托盘B与支撑点M的距离,记录相应的托盘B中的砝码质量,得到下表:
(1)把上表中(x,y)的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出其余的点,并用一条光滑曲线连接起来;观察所画的图象,猜测y与x之间的函数关系,求出该函数解析式;
(2)当托盘B向左移动(不超过点M)时,应往托盘B中添加砝码还是减少砝码?
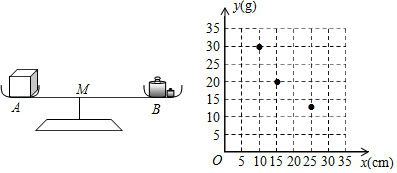
| 托盘B与点O的距离x(cm) | 10 | 15 | 20 | 25 | 30 |
| 托盘B中的砝码质量y(g) | 30 | 20 | 15 | 12 | 10 |
(2)当托盘B向左移动(不超过点M)时,应往托盘B中添加砝码还是减少砝码?

14.下列各组两项中,是同类项的是( )
| A. | -2xy与-3ab | B. | $\frac{1}{5}$abc与$\frac{1}{5}$ac | C. | xy与-xy | D. | 3x2y与3xy2 |
11.由四舍五入得到的近似数3.05万,下列说法正确的是( )
| A. | 精确到千分位 | B. | 精确到百分位 | C. | 精确到万分位 | D. | 精确到百位 |

 如图,正三角形ABC的边长为2,分别以A、B、C为圆心,1为半径画弧,与△ABC的内切圆O围成的图形为图中阴影部分,求S阴影.
如图,正三角形ABC的边长为2,分别以A、B、C为圆心,1为半径画弧,与△ABC的内切圆O围成的图形为图中阴影部分,求S阴影.