题目内容
17．两个相似三角形的最短边分别是5cm和3cm，它们的周长之差为12cm，那么小三角形的周长为（ ）| A． | 14cm | B． | 16cm | C． | 18cm | D． | 30cm |
分析 利用相似三角形（多边形）的周长的比等于相似比得到两三角形的周长的比为5：3，于是可设两三角形的周长分别为5xcm，3xcm，所以5x-3x=12，然后解方程求出x后就是3x即可．
解答 解：根据题意得两三角形的周长的比为5：3，
设两三角形的周长分别为5xcm，3xcm，
则5x-3x=12，解得x=6，
所以3x=18，
即小三角形的周长为18cm．
故选C．
点评 本题考查了相似三角形的性质：相似三角形的对应角相等，对应边的比相等；相似三角形（多边形）的周长的比等于相似比；相似三角形的面积的比等于相似比的平方．
练习册系列答案
相关题目
7．如图，在左边托盘A（固定）中放置一个重物，在右边托盘B（可左右移动）中放置一定质量的砝码，可使得仪器左右平衡，改变托盘B与支撑点M的距离，记录相应的托盘B中的砝码质量，得到下表：
（1）把上表中（x，y）的各组对应值作为点的坐标，在如图所示的平面直角坐标系中描出其余的点，并用一条光滑曲线连接起来；观察所画的图象，猜测y与x之间的函数关系，求出该函数解析式；
（2）当托盘B向左移动（不超过点M）时，应往托盘B中添加砝码还是减少砝码？
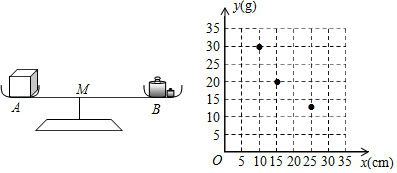
| 托盘B与点O的距离x（cm） | 10 | 15 | 20 | 25 | 30 |
| 托盘B中的砝码质量y（g） | 30 | 20 | 15 | 12 | 10 |
（2）当托盘B向左移动（不超过点M）时，应往托盘B中添加砝码还是减少砝码？
5．若一对相似三角形的相似比为1：3，则这对三角形的面积比为（ ）
| A． | 1：3 | B． | 3：1 | C． | 1：9 | D． | 1：$\sqrt{3}$ |
如图，在菱形ABCD中，AB=4，对角线AC、BD交于O点，E为AD延长线上一点，DE=2，直线OE分别交AB、CD于G、F．
2．$\frac{1}{2}$的相反数是（ ）
| A． | -2 | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 2 |
如图，正三角形ABC的边长为2，分别以A、B、C为圆心，1为半径画弧，与△ABC的内切圆O围成的图形为图中阴影部分，求S阴影．
如图，一艘渔船沿图中所示的折线由A航行到E，问船一共行驶了多少海里？
7．
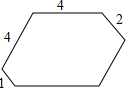如图，一个六边形的六个内角都是120°，其连续四条边的长依次为1，4，4，2；那么这个六边形的周长是（ ）
如图，一个六边形的六个内角都是120°，其连续四条边的长依次为1，4，4，2；那么这个六边形的周长是（ ）| A． | 19 | B． | 20 | C． | 25 | D． | 27 |