题目内容
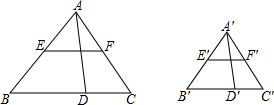如图，△ABC∽△A′BC′，AD、A′D′分别是这两个三角形的高，EF、E′F′分别是这两个三角形的中位线，| AD |
| A′D′ |
| EF |
| E′F′ |
考点：相似三角形的性质,三角形中位线定理
专题：常规题型
分析：先根据相似的性质由△ABC∽△A′BC′得到
=
，再根据三角形中位线性质得
=
=
，利用比例性质变形为
=
，所以
=
，然后根据相似三角形的对应线段（对应中线、对应角平分线、对应边上的高）的比也等于相似比得到
=
，于是有
=
．
| AB |
| A′B′ |
| BC |
| B′C′ |
| EF |
| BC |
| E′F′ |
| B′C′ |
| 1 |
| 2 |
| BC |
| B′C′ |
| EF |
| E′F′ |
| AB |
| A′B′ |
| EF |
| E′F′ |
| AB |
| A′B′ |
| AD |
| A′D′ |
| AB |
| A′B′ |
| EF |
| E′F′ |
解答：解：
与
相等．理由如下：
∵△ABC∽△A′BC′，
∴
=
，
∵EF、E′F′分别是这两个三角形的中位线，
∴
=
=
，
∴
=
，
∴
=
，
∵AD、A′D′分别是这两个三角形的高，
∴
=
，
∴
=
．
| AD |
| A′D′ |
| EF |
| E′F′ |
∵△ABC∽△A′BC′，
∴
| AB |
| A′B′ |
| BC |
| B′C′ |
∵EF、E′F′分别是这两个三角形的中位线，
∴
| EF |
| BC |
| E′F′ |
| B′C′ |
| 1 |
| 2 |
∴
| BC |
| B′C′ |
| EF |
| E′F′ |
∴
| AB |
| A′B′ |
| EF |
| E′F′ |
∵AD、A′D′分别是这两个三角形的高，
∴
| AB |
| A′B′ |
| AD |
| A′D′ |
∴
| AB |
| A′B′ |
| EF |
| E′F′ |
点评：本题考查了相似三角形的性质：相似三角形的对应角相等，对应边的比相等；相似三角形（多边形）的周长的比等于相似比；相似三角形的对应线段（对应中线、对应角平分线、对应边上的高）的比也等于相似比．也考查了三角形中位线性质．
练习册系列答案
名校课堂系列答案
相关题目
已知∠A=45°15′，∠B=45°12′18″，∠C=45.15°，则（ ）
| A、∠A＞∠B＞∠C |
| B、∠B＞∠A＞∠C |
| C、∠A＞∠C＞∠B |
| D、∠C＞∠A＞∠B |
如图，若DB⊥AE于B，DC⊥AF于C，延长BD交AF于点G，且DC=BD，∠ADG=120°，则下列结论正确的是：
如图，求sinA和sinB的值．
如图所示，△ABC中，∠ACB＞∠ABC，AE平分∠BAC，CD⊥AE于D，求证：∠ACD＞∠B．
如图所示是某长途汽车站旅客携带行李费用示意图．由图可知，行李的重量只要不超过
如图，∠1=∠2=∠3，写出图中的相似三角形，并说明理由．