题目内容
 如图,∠1=∠2=∠3,写出图中的相似三角形,并说明理由.
如图,∠1=∠2=∠3,写出图中的相似三角形,并说明理由.考点:相似三角形的判定
专题:
分析:根据两个三角形的两组角对应相等,那么这两个三角形互为相似三角形证明即可.
解答:解:△ABF∽△CDF,△ABC∽△ADE.
理由如下:∵∠2=∠3,∠AFD=∠EFB
∴△AFD∽△EFB,
∵△ABF∽△CDF,
∴∠B=∠D.
∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
∴△ABC∽△ADE.
理由如下:∵∠2=∠3,∠AFD=∠EFB
∴△AFD∽△EFB,
∵△ABF∽△CDF,
∴∠B=∠D.
∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
∴△ABC∽△ADE.
点评:本题考查相似三角形的判定定理,熟记判定定理,本题用到了两组角对应相等的两个三角形互为相似三角形.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
下面的说法正确的是( )
| A、-2不是单项式 |
| B、-a表示负数 |
| C、3πx2y的系数是3 |
| D、多项式x2+23x-1是二次三项式 |
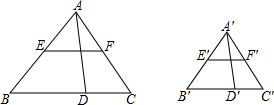 如图,△ABC∽△A′BC′,AD、A′D′分别是这两个三角形的高,EF、E′F′分别是这两个三角形的中位线,
如图,△ABC∽△A′BC′,AD、A′D′分别是这两个三角形的高,EF、E′F′分别是这两个三角形的中位线, 如图是二次函数y=ax2+3x-a2+4的图象,则a的值为
如图是二次函数y=ax2+3x-a2+4的图象,则a的值为