题目内容
如图，求sinA和sinB的值．考点：锐角三角函数的定义,勾股定理
专题：
分析：根据勾股定理，可得AB的长，根据正弦的定义，可得答案．
解答：解：由勾股定理，得
AB=
=
=
．
sinA=
=
=
，
sinB=
=
=
．
AB=
| AC2+BC2 |
| 52+32 |
| 34 |
sinA=
| BC |
| AB |
| 3 | ||
|
3
| ||
| 34 |
sinB=
| AC |
| AB |
| 5 | ||
|
5
| ||
| 34 |
点评：本题考查了锐角三角函数，利用了勾股定理，正弦函数的定义．
练习册系列答案
阅读快车系列答案
相关题目
在一幅长90cm，宽40cm的风景画的四周外围镶上一条宽度相同的金色纸边，制成一幅挂图，如果要求风景画的面积是整个挂图的80%．若设金色纸边的宽为xcm．根据题意列方程，并整理得（ ）
| A、x2-65x+350=0 |
| B、x2+65x-350=0 |
| C、x2+65x-225=0 |
| D、x2-65x+225=0 |
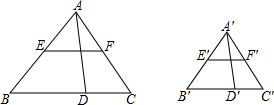如图，△ABC∽△A′BC′，AD、A′D′分别是这两个三角形的高，EF、E′F′分别是这两个三角形的中位线，
如图，四边形ABCD内接于⊙O，∠B=50°，∠ACD=25°，∠BAD=65°，求证：
如图，抛物线y=-2x2+4x与x轴交于O、B两点，C为顶点，点P为抛物线上一点，且△OPC是以OC为直角边的三角形，求P点坐标．