题目内容
如图，若DB⊥AE于B，DC⊥AF于C，延长BD交AF于点G，且DC=BD，∠ADG=120°，则下列结论正确的是：①∠GAB=60°；②∠BGF=120°；③AD=GD；④CG=AB．
考点：角平分线的性质
专题：
分析：先根据DB⊥AE于B，DC⊥AF于C，DC=BD得出AD是∠GAE的平分线，再由∠ADG=120°求出∠ADB的度数，由直角三角形的性质求出∠BAD的度数，进而可得出∠GAB的度数；同理可得出∠AGB的度数，由平角的定义得出∠BGF的度数；根据∠AGD与∠GAD相等可得出AD=GD；先根据等腰三角形的性质得出AC=CG，再由全等三角形的性质得出△ACD≌△ABD，故可得出AB=AC，由此可得出结论．
解答：解：∵DB⊥AE于B，DC⊥AF于C，DC=BD，
∴AD是∠GAE的平分线，
∴∠GAD=∠BAD．
∵∠ADG=120°，
∴∠ADB=180°-120°=60°，
∴∠BAD=90°-60°=30°，
∴∠GAB=2∠BAD=60°，故①正确；
∵DB⊥AE，
∴∠AGB=90°-∠GAB=90°-60°=30°，
∴∠BGF=180°-∠AGB=180°-30°=120°，故②正确；
∵由①、②知，∠CAD=∠AGB=30°，
∴AD=GD，故③正确；
∵AD=GD，DC⊥AF于C，
∴CD是AG的垂直平分线，
∴AC=CG．
在Rt△ACD与Rt△ABD中，
∴△ACD≌△ABD（HL），
∴AB=AC，
∴CG=AB，故④正确．
故答案为：①②③④．
解：∵DB⊥AE于B，DC⊥AF于C，DC=BD，∴AD是∠GAE的平分线，
∴∠GAD=∠BAD．
∵∠ADG=120°，
∴∠ADB=180°-120°=60°，
∴∠BAD=90°-60°=30°，
∴∠GAB=2∠BAD=60°，故①正确；
∵DB⊥AE，
∴∠AGB=90°-∠GAB=90°-60°=30°，
∴∠BGF=180°-∠AGB=180°-30°=120°，故②正确；
∵由①、②知，∠CAD=∠AGB=30°，
∴AD=GD，故③正确；
∵AD=GD，DC⊥AF于C，
∴CD是AG的垂直平分线，
∴AC=CG．
在Rt△ACD与Rt△ABD中，
|
∴△ACD≌△ABD（HL），
∴AB=AC，
∴CG=AB，故④正确．
故答案为：①②③④．
点评：本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．
练习册系列答案
相关题目
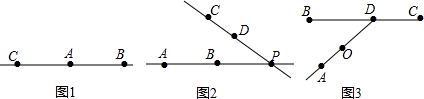
将图中标有弧线的角表示出来．
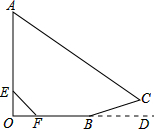小明利用旗杆在阳光下的影长来测量旗杆的高度．如图，旗杆OA直立在地面OD上，在某一时刻，他的影子由OB、BC两部分组成，测得OB为8m，BC为2m，其中BC在斜坡上，∠CBD=15°．小明在旗杆OA上取了一点E，使得OE为1m，测得OE的影长OF为1m．
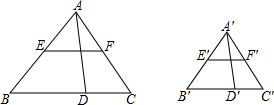如图，△ABC∽△A′BC′，AD、A′D′分别是这两个三角形的高，EF、E′F′分别是这两个三角形的中位线，
如图所示，∠AOB=90°，OE、OC分别是∠AOD、∠DOB的角平分线，求∠COE的度数．