题目内容
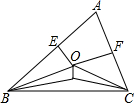 OE,OF分别是AB,AC边的中垂线,∠OBC,∠OCB的平分线相交于点I,试分析OI与BC位置关系,并给出证明.
OE,OF分别是AB,AC边的中垂线,∠OBC,∠OCB的平分线相交于点I,试分析OI与BC位置关系,并给出证明.考点:线段垂直平分线的性质,角平分线的性质
专题:
分析:首先连接OA,过点I作IM⊥OB于点M,过点I作IN⊥OC于点N,过点I作IG⊥BC于点G,由OE,OF分别是AB,AC边的中垂线,可得OA=OB=OC,又由∠OBC,∠OCB的平分线相交于点I,可得点I在∠BOC的角平分线上,然后由三线合一,证得结论.
解答: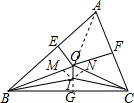 解:OI⊥BC.
解:OI⊥BC.
理由:连接OA,过点I作IM⊥OB于点M,过点I作IN⊥OC于点N,过点I作IG⊥BC于点G,
∵OE,OF分别是AB,AC边的中垂线,
∴OA=OB,OA=OC,
∴OB=OC,
∵∠OBC,∠OCB的平分线相交于点I,
∴IM=IG,IN=IG,
∴IM=IM,
∴点I在∠BOC的角平分线上,
∴OI⊥BC.
 解:OI⊥BC.
解:OI⊥BC.理由:连接OA,过点I作IM⊥OB于点M,过点I作IN⊥OC于点N,过点I作IG⊥BC于点G,
∵OE,OF分别是AB,AC边的中垂线,
∴OA=OB,OA=OC,
∴OB=OC,
∵∠OBC,∠OCB的平分线相交于点I,
∴IM=IG,IN=IG,
∴IM=IM,
∴点I在∠BOC的角平分线上,
∴OI⊥BC.
点评:此题考查了线段垂直平分线的性质以及角平分线的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,若CD平分∠ACE,BD平分∠ABC,∠A=45°,则∠D=
如图,若CD平分∠ACE,BD平分∠ABC,∠A=45°,则∠D=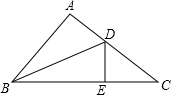 如图,BD是△ABC的角平分线,DE⊥BC于E,若S△ABC=60cm2,AB=12cm,BC=18cm,则S△DBC=
如图,BD是△ABC的角平分线,DE⊥BC于E,若S△ABC=60cm2,AB=12cm,BC=18cm,则S△DBC= 如图,已知Rt△ABC,∠BAC=90°,点D在BC上,AD=DC,DE⊥AB,交AB于O,BE∥AD.求证:∠BED=∠C.
如图,已知Rt△ABC,∠BAC=90°,点D在BC上,AD=DC,DE⊥AB,交AB于O,BE∥AD.求证:∠BED=∠C.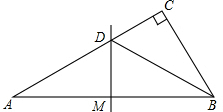 如图所示,已知△ABC中,∠C=90°,AB的垂直平分线DM交AC于D,垂足为M.
如图所示,已知△ABC中,∠C=90°,AB的垂直平分线DM交AC于D,垂足为M.