题目内容
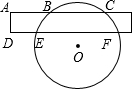 如图,为了测量一圆形工件的直径,一同学想利用一宽为1cm的矩形纸条放在这个圆形工件上,量得AB=BC=6cm,DE=5cm,求该工件的直径的长度.
如图,为了测量一圆形工件的直径,一同学想利用一宽为1cm的矩形纸条放在这个圆形工件上,量得AB=BC=6cm,DE=5cm,求该工件的直径的长度.考点:垂径定理的应用,勾股定理
专题:
分析:过O作OZ⊥BC于Z,交EF于G,求出OZ⊥EG,由垂径定理求出BZ=CZ=
BC=3cm,求出EG=4cm,设OG=xcm,半径为Rcm,在Rt△OEG和Rt△OBZ中,由勾股定理得出方程R2=x2+43=(x+1)2+32,求出即可.
| 1 |
| 2 |
解答: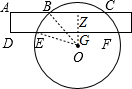 解:过O作OZ⊥BC于Z,交EF于G,
解:过O作OZ⊥BC于Z,交EF于G,
根据矩形性质得:AC∥AE,
即OZ⊥EG,
则由垂径定理得:BZ=CZ=
BC=
×6cm=3cm,
则AZ=DG=6cm+3cm=9cm,
所以EG=9cm-5cm=4cm,
设OG=xcm,半径为Rcm,
在Rt△OEG和Rt△OBZ中,由勾股定理得:R2=x2+42=(x+1)2+32,
解得:x=3,R=5,
故该工件的直径的长度为2×5cm=10cm.
 解:过O作OZ⊥BC于Z,交EF于G,
解:过O作OZ⊥BC于Z,交EF于G,根据矩形性质得:AC∥AE,
即OZ⊥EG,
则由垂径定理得:BZ=CZ=
| 1 |
| 2 |
| 1 |
| 2 |
则AZ=DG=6cm+3cm=9cm,
所以EG=9cm-5cm=4cm,
设OG=xcm,半径为Rcm,
在Rt△OEG和Rt△OBZ中,由勾股定理得:R2=x2+42=(x+1)2+32,
解得:x=3,R=5,
故该工件的直径的长度为2×5cm=10cm.
点评:本题考查了垂径定理,勾股定理等知识点的应用,解此题的关键是能得出关于x的方程,题目比较典型,难度适中.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
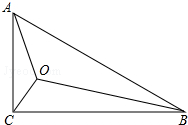 在Rt△ABC中,∠C=90°,AC=1,BC=
在Rt△ABC中,∠C=90°,AC=1,BC= 如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( )
如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( ) 如图,已知四边形ABCD中,AC平分∠BAD,DC=BC,求∠ADC+∠ABC的度数.
如图,已知四边形ABCD中,AC平分∠BAD,DC=BC,求∠ADC+∠ABC的度数. 如图,已知Rt△ABC是⊙O的内接三角形,其中直角边AC=8,BC=6,则⊙O的半径是
如图,已知Rt△ABC是⊙O的内接三角形,其中直角边AC=8,BC=6,则⊙O的半径是