题目内容
 如图,已知四边形ABCD中,AC平分∠BAD,DC=BC,求∠ADC+∠ABC的度数.
如图,已知四边形ABCD中,AC平分∠BAD,DC=BC,求∠ADC+∠ABC的度数.考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:过C作CF⊥AB于F,CE⊥AD交AD延长线于E,根据角平分线性质求出CE=CF,根据HL证Rt△DEC≌Rt△BFC,推出∠ABC=∠EDC即可.
解答:解:
过C作CF⊥AB于F,CE⊥AD交AD延长线于E,
则∠E=∠CFB=90°,
∵AC平分∠BAD,
∴CE=CF,
在Rt△DEC和Rt△BFC中
∴Rt△DEC≌Rt△BFC(HL),
∴∠ABC=∠EDC,
∵∠ADC+∠EDC=180°,
∴∠ADC+∠ABC=180°.

过C作CF⊥AB于F,CE⊥AD交AD延长线于E,
则∠E=∠CFB=90°,
∵AC平分∠BAD,
∴CE=CF,
在Rt△DEC和Rt△BFC中
|
∴Rt△DEC≌Rt△BFC(HL),
∴∠ABC=∠EDC,
∵∠ADC+∠EDC=180°,
∴∠ADC+∠ABC=180°.
点评:本题考查了全等三角形的性质和判定的应用,解此题的关键是作辅助线后求出Rt△DEC≌Rt△BFC,题目比较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图a,b为数轴上的两点,下列结论正确的是( )
如图a,b为数轴上的两点,下列结论正确的是( )| A、b<-a<0<a<-b |
| B、a<-b<0<b<-a |
| C、a<b<0<-a<-b |
| D、-a<-b<0<b<a |
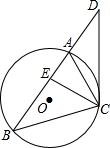 如图,已知CD是△ABC的外接圆的切线,C为切点,BA的延长线与切线CD相交于点D,点E在边AB上,且DE=DC.求证:CE平分∠ACB.
如图,已知CD是△ABC的外接圆的切线,C为切点,BA的延长线与切线CD相交于点D,点E在边AB上,且DE=DC.求证:CE平分∠ACB.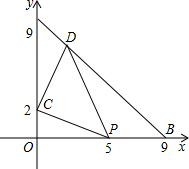 如图,在△AOB中,OA=0B=9,点C的坐标为(0,2),点P是OB上一动点,连接CP,将CP绕C点逆时针旋转90°得到线段CD,使点D恰好落在AB上,求点D的坐标.
如图,在△AOB中,OA=0B=9,点C的坐标为(0,2),点P是OB上一动点,连接CP,将CP绕C点逆时针旋转90°得到线段CD,使点D恰好落在AB上,求点D的坐标.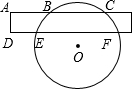 如图,为了测量一圆形工件的直径,一同学想利用一宽为1cm的矩形纸条放在这个圆形工件上,量得AB=BC=6cm,DE=5cm,求该工件的直径的长度.
如图,为了测量一圆形工件的直径,一同学想利用一宽为1cm的矩形纸条放在这个圆形工件上,量得AB=BC=6cm,DE=5cm,求该工件的直径的长度.