题目内容
某金鱼养殖户用一种可重复使用的材料围建了一个直径为16米的圆形养鱼池,现因养殖的需要,必须将其改建成两个半径不等的圆形鱼池,在既不增加围建材料也不浪费的前提下(提示:两圆的周长和与大圆周长相等),为了方便管理让两圆相切.当小圆半径为多少时,鱼池占地面积为36π平方米?
考点:相切两圆的性质
专题:应用题
分析:利用已知直径求出圆的周长,进而得出两圆半径的和,再利用两圆面积和为36π平方米得出答案即可.
解答:解:大圆直径16m,
∴大圆的周长C1=2πr1=2π×
=16π,
设两圆中小圆半径为r2,两圆中较大的圆半径为r3,
∵改建后两圆的周长和与大圆周长相等,
∴2πr2+2πr3=16π,
解得:r2+r3=8 (即两圆半径之和与最先大圆的半径相等),
∵两圆面积之和为36π,
∴有πr22+πr32=πr22+π(8-r2)2=36π,
化简有r22+(8-r2)2=36,
解得:r2=4+
或4-
∵题中求的是小圆半径,
∴只能取r2=4-
,而4+
舍去.
∴大圆的周长C1=2πr1=2π×
| d1 |
| 2 |
设两圆中小圆半径为r2,两圆中较大的圆半径为r3,
∵改建后两圆的周长和与大圆周长相等,
∴2πr2+2πr3=16π,
解得:r2+r3=8 (即两圆半径之和与最先大圆的半径相等),
∵两圆面积之和为36π,
∴有πr22+πr32=πr22+π(8-r2)2=36π,
化简有r22+(8-r2)2=36,
解得:r2=4+
| 2 |
| 2 |
∵题中求的是小圆半径,
∴只能取r2=4-
| 2 |
| 2 |
点评:此题主要考查了相切两圆的性质以及圆的面积公式,得出两半径的关系是解题关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
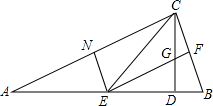 如图,CD是△ABC的高,∠A=22.5°,边AC的垂直平分线交AB于点E,EF⊥BC,交CD于点G,垂足为F.求证:DB=DG.
如图,CD是△ABC的高,∠A=22.5°,边AC的垂直平分线交AB于点E,EF⊥BC,交CD于点G,垂足为F.求证:DB=DG. 如图,已知PB切⊙O于B,PDC是割线,弦AB∥CD,M为
如图,已知PB切⊙O于B,PDC是割线,弦AB∥CD,M为
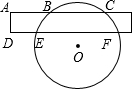 如图,为了测量一圆形工件的直径,一同学想利用一宽为1cm的矩形纸条放在这个圆形工件上,量得AB=BC=6cm,DE=5cm,求该工件的直径的长度.
如图,为了测量一圆形工件的直径,一同学想利用一宽为1cm的矩形纸条放在这个圆形工件上,量得AB=BC=6cm,DE=5cm,求该工件的直径的长度.