题目内容
已知在Rt△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C对应的边,若a+b=10,∠A=60°,则斜边c= .
考点:含30度角的直角三角形,勾股定理
专题:
分析:根据直角三角形两锐角互余求出∠B=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得b=
c,然后表示出a,再利用勾股定理列方程求解即可.
| 1 |
| 2 |
解答:解:∵∠C=90°,∠A=60°,
∴∠B=90°-60°=30°,
∴b=
c,
∵a+b=10,
∴a=10-
c,
由勾股定理得,a2+b2=c2,
∴(10-
c)2+(
c)2=c2,
整理得,c2+20c-200=0,
解得c1=-10+10
,c2=-10-10
(舍去).
故答案为:-10+10
.
∴∠B=90°-60°=30°,
∴b=
| 1 |
| 2 |
∵a+b=10,
∴a=10-
| 1 |
| 2 |
由勾股定理得,a2+b2=c2,
∴(10-
| 1 |
| 2 |
| 1 |
| 2 |
整理得,c2+20c-200=0,
解得c1=-10+10
| 3 |
| 3 |
故答案为:-10+10
| 3 |
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半,勾股定理,熟记性质并用c表示出a、b,然后列出方程是解题的关键.

练习册系列答案
相关题目
 如图a,b为数轴上的两点,下列结论正确的是( )
如图a,b为数轴上的两点,下列结论正确的是( )| A、b<-a<0<a<-b |
| B、a<-b<0<b<-a |
| C、a<b<0<-a<-b |
| D、-a<-b<0<b<a |
绝对值等于2008的数是( )
| A、2008 | ||
| B、-2008 | ||
| C、±2008 | ||
D、
|
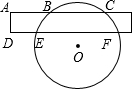 如图,为了测量一圆形工件的直径,一同学想利用一宽为1cm的矩形纸条放在这个圆形工件上,量得AB=BC=6cm,DE=5cm,求该工件的直径的长度.
如图,为了测量一圆形工件的直径,一同学想利用一宽为1cm的矩形纸条放在这个圆形工件上,量得AB=BC=6cm,DE=5cm,求该工件的直径的长度.