题目内容
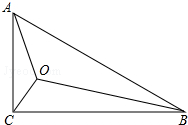 在Rt△ABC中,∠C=90°,AC=1,BC=
在Rt△ABC中,∠C=90°,AC=1,BC=| 3 |
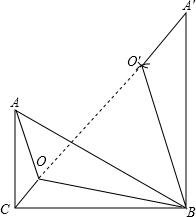
(1)用尺规作图作出△A′O′B;
(2)证明:点C、O、O′和A′四点共线;
(3)求OA+OB+OC的值.
考点:几何变换综合题
专题:
分析:(1)解直角三角形求出∠ABC=30°,然后过点B作BC的垂线,在截取A′B=AB,再以点A′为圆心,以AO为半径画弧,以点B为圆心,以BO为半径画弧,两弧相交于点O′,连接A′O′、BO′,即可得到△A′O′B;
(2)根据旋转角与∠ABC的度数,相加即可得到∠A′BC;
(3)根据直角三角形30°角所对的直角边等于斜边的一半求出AB=2AC,即A′B的长,再根据旋转的性质求出△BOO′是等边三角形,根据等边三角形的三条边都相等可得BO=OO′,等边三角形三个角都是60°求出∠BOO′=∠BO′O=60°,然后求出C、O、A′、O′四点共线,再利用勾股定理列式求出A′C,从而得到OA+OB+OC=A′C.
(2)根据旋转角与∠ABC的度数,相加即可得到∠A′BC;
(3)根据直角三角形30°角所对的直角边等于斜边的一半求出AB=2AC,即A′B的长,再根据旋转的性质求出△BOO′是等边三角形,根据等边三角形的三条边都相等可得BO=OO′,等边三角形三个角都是60°求出∠BOO′=∠BO′O=60°,然后求出C、O、A′、O′四点共线,再利用勾股定理列式求出A′C,从而得到OA+OB+OC=A′C.
解答:解:(1)∵∠C=90°,AC=1,BC=
,
∴tan∠ABC=
=
=
,
∴∠ABC=30°,
∵△AOB绕点B顺时针方向旋转60°,
∠A′BC=∠ABC+60°=30°+60°=90°,
∴A′B⊥CB,
过点B作BC的垂线,在截取A′B=AB,
再以点A′为圆心,以AO为半径画弧,
以点B为圆心,以BO为半径画弧,
两弧相交于点O′,连接A′O′、BO′,
即△A′O′B如图所示;
(2)证明:∵∠C=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
(3)在Rt△A′BC中,A′C=
=
=
,
∴OA+OB+OC=A′O′+OO′+OC=A′C=
.
| 3 |

∴tan∠ABC=
| AC |
| BC |
| 1 | ||
|
| ||
| 3 |
∴∠ABC=30°,
∵△AOB绕点B顺时针方向旋转60°,
∠A′BC=∠ABC+60°=30°+60°=90°,
∴A′B⊥CB,
过点B作BC的垂线,在截取A′B=AB,
再以点A′为圆心,以AO为半径画弧,
以点B为圆心,以BO为半径画弧,
两弧相交于点O′,连接A′O′、BO′,
即△A′O′B如图所示;
(2)证明:∵∠C=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
(3)在Rt△A′BC中,A′C=
| BC2+A′B2 |
|
| 7 |
∴OA+OB+OC=A′O′+OO′+OC=A′C=
| 7 |
点评:本题考查了利用旋转变换作图,旋转变换的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,勾股定理,等边三角形的判定与性质,综合性较强,最后一问求出C、O、A′、O′四点共线是解题的关键.

练习册系列答案
相关题目
已知x2+3x+5=3,那么整式2-3x2-9x的值为( )
| A、0 | B、2 | C、-4 | D、8 |
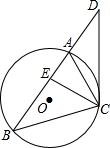 如图,已知CD是△ABC的外接圆的切线,C为切点,BA的延长线与切线CD相交于点D,点E在边AB上,且DE=DC.求证:CE平分∠ACB.
如图,已知CD是△ABC的外接圆的切线,C为切点,BA的延长线与切线CD相交于点D,点E在边AB上,且DE=DC.求证:CE平分∠ACB.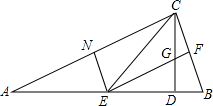 如图,CD是△ABC的高,∠A=22.5°,边AC的垂直平分线交AB于点E,EF⊥BC,交CD于点G,垂足为F.求证:DB=DG.
如图,CD是△ABC的高,∠A=22.5°,边AC的垂直平分线交AB于点E,EF⊥BC,交CD于点G,垂足为F.求证:DB=DG.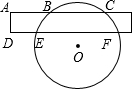 如图,为了测量一圆形工件的直径,一同学想利用一宽为1cm的矩形纸条放在这个圆形工件上,量得AB=BC=6cm,DE=5cm,求该工件的直径的长度.
如图,为了测量一圆形工件的直径,一同学想利用一宽为1cm的矩形纸条放在这个圆形工件上,量得AB=BC=6cm,DE=5cm,求该工件的直径的长度.