题目内容
5.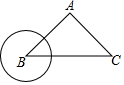 如图,△ABC中,AB=AC=5,BC=8,⊙B的半径为2,圆心B从点B出发,沿着线段BC向右平移,⊙B随着点B的平移而以相同的速度平移.当⊙B与边AB相切时,⊙B平移的距离是$\frac{10}{3}$.
如图,△ABC中,AB=AC=5,BC=8,⊙B的半径为2,圆心B从点B出发,沿着线段BC向右平移,⊙B随着点B的平移而以相同的速度平移.当⊙B与边AB相切时,⊙B平移的距离是$\frac{10}{3}$.
分析 如图,作AH⊥BC于H,设切点为E,连接B′E.根据sinB=$\frac{B′E}{BB′}$=$\frac{AH}{AB}$,求出AH、BH即可解决问题.
解答 解:如图,作AH⊥BC于H,设切点为E,连接B′E.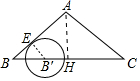
∵AB=AC=5,AH⊥BC,
∴BH=CH=4,
在Rt△ABH中,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=3,
∵∠BEB′=∠AHB=90°,
∴sinB=$\frac{B′E}{BB′}$=$\frac{AH}{AB}$,
∴$\frac{2}{BB′}$=$\frac{3}{5}$,
∴BB′=$\frac{10}{3}$.
故答案为$\frac{10}{3}$.
点评 本题考查切线的性质、等腰三角形的性质、勾股定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.已知⊙O的面积为9πcm2,若圆心O到直线的距离为3cm,则直线与⊙O的位置关系是( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无 |
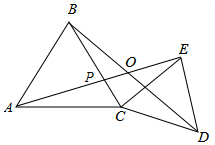 如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB=60°.
如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB=60°.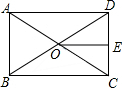 如图,在矩形ABCD中,AC、BD相交于点O,OE⊥CD.求证:OE=$\frac{1}{2}$AD.
如图,在矩形ABCD中,AC、BD相交于点O,OE⊥CD.求证:OE=$\frac{1}{2}$AD.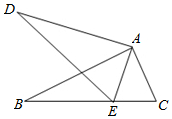 如图,在△ABC和△ADE中,点E在BC边上,∠B=∠D,AB=AD,∠BAD=∠CAE.
如图,在△ABC和△ADE中,点E在BC边上,∠B=∠D,AB=AD,∠BAD=∠CAE.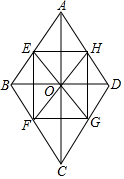 已知菱形ABCD的对角线相交于O,点E、F分别在边AB、BC上,且BE=BF,射线EO、FO分别交边CD、AD于G、H.
已知菱形ABCD的对角线相交于O,点E、F分别在边AB、BC上,且BE=BF,射线EO、FO分别交边CD、AD于G、H.