题目内容
8.Rt△ABC中,∠C=90°,AC=15,AB=25,则Rt△ABC的面积是150.分析 首先根据勾股定理求得BC的长度,然后根据直角三角形的面积公式进行解答.
解答 解:∵Rt△ABC中,∠C=90°,AC=15,AB=25,
∴由勾股定理得:BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{2{5}^{2}-1{5}^{2}}$=20.
∴Rt△ABC的面积=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×15×20=150.
故答案是:150.
点评 本题考查了勾股定理,三角形的面积.注意:勾股定理应用于直角三角形中,所以在解题过程中,必须指明△ABC是直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列计算正确的是( )
| A. | $\root{3}{-8}$=-2 | B. | $\sqrt{36}$=±6 | C. | $\sqrt{3}$$+\sqrt{2}$=$\sqrt{5}$ | D. | $\sqrt{{a}^{2}}$=a |
17. 如图,在一块两边长分别为AB=6m,BC=8m的长方形草地上,顶点A、B、C、D处各居住着一只蚂蚁,居住在顶点A处的蚂蚁准备拜访居住在C点的蚂蚁,它到达C点的行程最少为( )
如图,在一块两边长分别为AB=6m,BC=8m的长方形草地上,顶点A、B、C、D处各居住着一只蚂蚁,居住在顶点A处的蚂蚁准备拜访居住在C点的蚂蚁,它到达C点的行程最少为( )
 如图,在一块两边长分别为AB=6m,BC=8m的长方形草地上,顶点A、B、C、D处各居住着一只蚂蚁,居住在顶点A处的蚂蚁准备拜访居住在C点的蚂蚁,它到达C点的行程最少为( )
如图,在一块两边长分别为AB=6m,BC=8m的长方形草地上,顶点A、B、C、D处各居住着一只蚂蚁,居住在顶点A处的蚂蚁准备拜访居住在C点的蚂蚁,它到达C点的行程最少为( )| A. | 7m | B. | 8m | C. | 9m | D. | 10m |
18.如果把分式$\frac{x+2y}{x+y}$中的x、y的值都变为原来的10倍,那么分式的值( )
| A. | 变成原来的10倍 | B. | 缩小为原来的10倍 | ||
| C. | 是原来的$\frac{2}{3}$ | D. | 不变 |
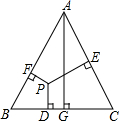 如图,已知等边三角形ABC中,AG⊥BC,PD⊥BC,PE⊥AC,PF⊥AB.求证:PD+PE+PF=AG.
如图,已知等边三角形ABC中,AG⊥BC,PD⊥BC,PE⊥AC,PF⊥AB.求证:PD+PE+PF=AG.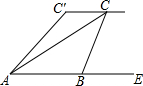 如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100m.当气球沿与BA平行的路线飘移10秒后到达C′处时,在A处测得气球的仰角为45°.求∠ACC′的度数.
如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100m.当气球沿与BA平行的路线飘移10秒后到达C′处时,在A处测得气球的仰角为45°.求∠ACC′的度数.