Question

12．如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（-3，2），B（0，4），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A₁B₁C；平移△ABC，若点A的对应点A₂的坐标为（0，-4），画出平移后对应的△A₂B₂C₂；
（2）在x轴上有一点P，使得PA+PB的值最小，请求出点P的坐标．

Answer 1

分析 （1）根据图形旋转与平移的性质画出图形即可；
（2）作点A关于x轴的对称点A′，连接A′B交x轴于点P，利用待定系数法求出直线A′B的解析式，进而可得出P点坐标．

解答 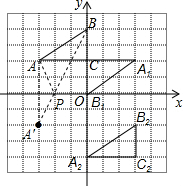解：（1）如图所示；

（2）作点A关于x轴的对称点A′，连接A′B交x轴于点P，则点P即为所求点，
∵A（-3，2），
∴A′（-3，-2）．
设直线A′B的解析式为y=kx+b（k≠0），
∵A′（-3，-2），B（0，4），
∴$\left\{\begin{array}{l}-3k+b=-2\\ b=4\end{array}\right.$，解得$\left\{\begin{array}{l}k=2\\ b=4\end{array}\right.$，
∴直线A′B的解析式为y=2x+4，
∵当y=0时，x=-2，
∴P（-2，0）．

点评 本题考查的是作图-旋转变换，熟知图形旋转不变性的性质是解答此题的关键．