题目内容
7．点P（2m-1，3）在第二象限，则m的取值范围是m＜$\frac{1}{2}$；点A（x-1，2-x）在第四象限，则实数x的取值范围是1＜x＜2．分析 首先根据第二象限内点的坐标符号可得到2m-1＜0，然后再解即可；根据第四象限内点的坐标符号可得x-1＞0，2-x＜0，再解不等式组即可．
解答 解：∵点P（2m-1，3）在第二象限，
∴2m-1＜0，
∴m＜$\frac{1}{2}$，
故答案为：m$＜\frac{1}{2}$；
∵点A（x-1，2-x）在第四象限，
∴x-1＞0，2-x＜0，
解得：1＜x＜2，
故答案为：1＜x＜2．
点评 此题主要考查了点的坐标，关键是掌握第一象限内点的坐标符号（+，+），第二象限内点的坐标符号（-，+），第三象限内点的坐标符号（-，-），第四象限内点的坐标符号（+，-）．
练习册系列答案
相关题目
17．下列事件：
（1）抛掷1枚硬币正面朝上；
（2）任意两正整数的和大于1；
（3）打开电视正在播放新闻联播；
（4）长为3cm、5cm、9cm的三条线段能围成一个三角形．
其中确定事件有（ ）
（1）抛掷1枚硬币正面朝上；
（2）任意两正整数的和大于1；
（3）打开电视正在播放新闻联播；
（4）长为3cm、5cm、9cm的三条线段能围成一个三角形．
其中确定事件有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
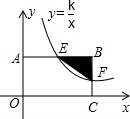如图，反比例函数y=$\frac{k}{x}$（k＞0）的图象与矩形ABCO的两边相交于E，F两点，若E是AB的中点，S△BEF=1，则k的值为4．
如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（-3，2），B（0，4），C（0，2）．
如图是汽车加油站在加油过程中，加油器仪表某一瞬间的显示，请你结合图片信息，解答下列问题：