题目内容
1.下列化简:①$\sqrt{128{a}^{2}{b}^{3}{c}^{5}}$=$\sqrt{64×2{a}^{2}{b}^{3}{c}^{5}}$=8abc2$\sqrt{2bc}$;
②$\sqrt{16{a}^{3}+32{a}^{2}}$=$\sqrt{16{a}^{2}(a+2)}$=4a$\sqrt{a+2}$;
③5$\sqrt{\frac{2}{5}}$=5×$5\sqrt{10}$=25$\sqrt{10}$;
④3$\sqrt{\frac{1}{3}}$=$\sqrt{3}$.
其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据化简二次根式的步骤,逐一判断出每个根式的化简结果是否正确,进而判断出正确的个数是多少即可.
解答 解:∵$\sqrt{128{a}^{2}{b}^{3}{c}^{5}}$=$\sqrt{64×2{a}^{2}{b}^{3}{c}^{5}}$=8abc2$\sqrt{2bc}$,
∴①正确.
∵$\sqrt{16{a}^{3}+32{a}^{2}}$=$\sqrt{16{a}^{2}(a+2)}$=4|a|$\sqrt{a+2}$,
∴②不正确.
∵5$\sqrt{\frac{2}{5}}$=5×$\frac{\sqrt{10}}{5}$=$\sqrt{10}$,
∴③不正确.
∵3$\sqrt{\frac{1}{3}}$=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
∴④正确.
综上,可得
正确的有两个:①④.
故选:B.
点评 此题主要考查了二次根式的性质和化简,要熟练掌握,解答此题的关键是要明确化简二次根式的步骤:①把被开方数分解因式;②利用积的算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
10.下列计算正确的是( )
| A. | $\sqrt{{{(-6)}^2}}$=-6 | B. | -$\sqrt{{{(-6)}^2}}$=-6 | C. | $\sqrt{{{(-6)}^2}}$=±6 | D. | $\sqrt{6^2}$=±6 |
 如图是一块长方形ABCD的场地,长AB=10米,宽AD=6米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为40平方米.
如图是一块长方形ABCD的场地,长AB=10米,宽AD=6米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为40平方米.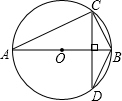 如右图,AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,那么sin∠ABD的值是$\frac{4}{5}$.
如右图,AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,那么sin∠ABD的值是$\frac{4}{5}$.