题目内容
4.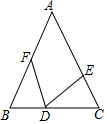 如图,在△ABC中,∠B=∠C,BD=CE,CD=BF,则∠EDF等于( )
如图,在△ABC中,∠B=∠C,BD=CE,CD=BF,则∠EDF等于( )| A. | 90°-∠A | B. | 90°-$\frac{1}{2}$∠A | C. | 180°-2∠A | D. | 45°-$\frac{1}{2}$∠A |
分析 先证明△BDF≌△CDF(SAS),然后根据∠FDC=∠EDF+∠EDC=∠BFD+∠B,即可求出∠EDF的度数.
解答 解:在△BDF与△CDF中,
$\left\{\begin{array}{l}{BF=CD}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$
∴△BDF≌△CDF(SAS)
∴∠BFD=∠EDC,
∵∠B=$\frac{180°-∠A}{2}$=90°-$\frac{∠A}{2}$
∴∠FDC=∠EDF+∠EDC=∠BFD+∠B,
∴∠EDF=90°-$\frac{∠A}{2}$
故选(B)
点评 本题考查全等三角形的判定,解题的关键是熟练运用全等三角形判定方法,本题属于基础题型.

练习册系列答案
相关题目
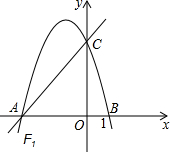 如图,直线y=$\frac{4}{3}$x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
如图,直线y=$\frac{4}{3}$x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).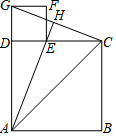 如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A、D、G在同一直线上,且AD=3,DE=1,连接AC、CG、AE,并延长AE交OG于点H.
如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A、D、G在同一直线上,且AD=3,DE=1,连接AC、CG、AE,并延长AE交OG于点H.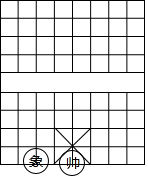 如图,中国象棋中对“象”的走法有一定的限制,只能走“田”字.若此时“象”的坐标为(-2,-4)“帅”的坐标为(0,-4),试写出此“象”下一步可能走到的各位置的坐标.
如图,中国象棋中对“象”的走法有一定的限制,只能走“田”字.若此时“象”的坐标为(-2,-4)“帅”的坐标为(0,-4),试写出此“象”下一步可能走到的各位置的坐标.