题目内容
14.计算或解方程(1)(-$\frac{1}{2}$)-2+|3tan30°-1|-(π-3)°;
(2)$\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3.
分析 (1)原式利用零指数幂、负整数指数幂法则,以及绝对值的代数意义化简即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=4+$\sqrt{3}$-1-1=2+$\sqrt{3}$;
(2)去分母得:1=x-1-3x+6,
解得:x=2,
经检验x=2是增根,分式方程无解.
点评 此题考查了解分式方程,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
4.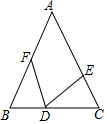 如图,在△ABC中,∠B=∠C,BD=CE,CD=BF,则∠EDF等于( )
如图,在△ABC中,∠B=∠C,BD=CE,CD=BF,则∠EDF等于( )
 如图,在△ABC中,∠B=∠C,BD=CE,CD=BF,则∠EDF等于( )
如图,在△ABC中,∠B=∠C,BD=CE,CD=BF,则∠EDF等于( )| A. | 90°-∠A | B. | 90°-$\frac{1}{2}$∠A | C. | 180°-2∠A | D. | 45°-$\frac{1}{2}$∠A |
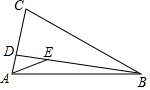 在△ABC中,AB=BC,∠ABC=30°,D为AC边上一点,连接BD,在BD上取点E,连接AE,若∠AED=30°,DE=2,△BDC的面积为12,则线段BE的长度为6.
在△ABC中,AB=BC,∠ABC=30°,D为AC边上一点,连接BD,在BD上取点E,连接AE,若∠AED=30°,DE=2,△BDC的面积为12,则线段BE的长度为6.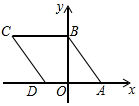 如图,四边形ABCD是菱形,A(3,0),B(0,4),则点C的坐标是(-5,4).
如图,四边形ABCD是菱形,A(3,0),B(0,4),则点C的坐标是(-5,4).