题目内容
如图，AB是⊙O的直径，∠C=25°，则∠ABD=（ ）| A、25° | B、55° |
| C、65° | D、75° |
考点：圆周角定理
专题：
分析：连接OD，可求得∠DOB=2∠C=50°，在△DOB中利用等腰三角形的性质结合三角形内角和定理可求得∠ABD．
解答：
解：
连接OD，则∠DOB=2∠C=50°，
∵OD=OB，
∴∠ABD=
=65°，
故选C．
解：连接OD，则∠DOB=2∠C=50°，
∵OD=OB，
∴∠ABD=
| 180°-50° |
| 2 |
故选C．
点评：本题主要考查圆周角定理，掌握同圆中同弧所对的圆周角是圆心角的一半是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，四边形BDEF内接于圆O中，分别延长DE、BF交于点C，直径AB⊥DE于点H．求证：∠1=∠2．一个多边形的内角和等于1440°，则它是（ ）边形．
| A、11 | B、6 | C、5 | D、8 |
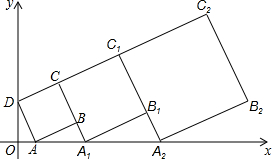在平面坐标系xOy中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A2，作正方形A2B2C2C1，求C2坐标．