题目内容
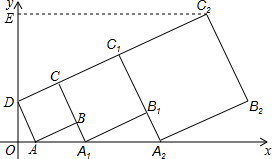
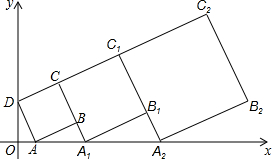 在平面坐标系xOy中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,求C2坐标.
在平面坐标系xOy中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,求C2坐标.考点:正方形的性质
专题:规律型
分析:根据点A、D的坐标求出OA、OD,利用勾股定理列式求出AD,再求出△AOD与△A1BA相似,根据相似三角形对应边成比例求出A1B,然后求出第二个正方形的边长,同理求出第三个正方形的边长,过点C2作C2E⊥y轴于E,利用相似三角形对应边成比例求出DE、C2E,再求出OE,然后写出点C2的坐标即可.
解答:解:∵点A的坐标为(1,0),点D的坐标为(0,2),
∴OA=1,OD=2,
由勾股定理得,AD=
=
,
∵四边形ABCD是正方形,
∴∠DAB=90°,AB=BC=AD,
∴∠BAA1=∠ODA,
又∵∠AOD=∠A1BA=90°,
∴△AOD∽△A1BA,
∴
=
=
,
∴A1B=
AB=
,
∴第二个正方形的边长A1C=BC+A1B=
+
=
,
同理可得第三个正方形的边长A2C1=
×
=
,
∴DC2=
+
+
=
,
过点C2作C2E⊥y轴于E,
易得△AOD∽△DEC2,
所以,
=
=
,
即
=
=
,
解得DE=
,C2E=
,
所以,OE=2+
=
,
所以,点C2的坐标为(
,
).
∴OA=1,OD=2,
由勾股定理得,AD=
| 12+22 |
| 5 |
∵四边形ABCD是正方形,
∴∠DAB=90°,AB=BC=AD,
∴∠BAA1=∠ODA,
又∵∠AOD=∠A1BA=90°,
∴△AOD∽△A1BA,
∴
| A1B |
| AB |
| OA |
| OD |
| 1 |
| 2 |

∴A1B=
| 1 |
| 2 |
| ||
| 2 |
∴第二个正方形的边长A1C=BC+A1B=
| 5 |
| ||
| 2 |
3
| ||
| 2 |
同理可得第三个正方形的边长A2C1=
| 3 |
| 2 |
3
| ||
| 2 |
| 9 |
| 4 |
| 5 |
∴DC2=
| 5 |
3
| ||
| 2 |
| 9 |
| 4 |
| 5 |
| 19 |
| 4 |
| 5 |
过点C2作C2E⊥y轴于E,
易得△AOD∽△DEC2,
所以,
| DE |
| OA |
| C2E |
| OD |
| DC2 |
| AD |
即
| DE |
| 1 |
| C2E |
| 2 |
| ||||
|
解得DE=
| 9 |
| 4 |
| 9 |
| 2 |
所以,OE=2+
| 9 |
| 4 |
| 17 |
| 4 |
所以,点C2的坐标为(
| 17 |
| 4 |
| 9 |
| 2 |
点评:本题考查了正方形的性质,勾股定理,相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键,难点在于分别求出正方形的边长并判断出前后正方形边长的变化规律.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,∠C=25°,则∠ABD=( )
如图,AB是⊙O的直径,∠C=25°,则∠ABD=( )| A、25° | B、55° |
| C、65° | D、75° |
如果多项式P=a2+2b2+2a+4b+2015,则P的最小值是( )
| A、2011 | B、2012 |
| C、2013 | D、2014 |