题目内容
17.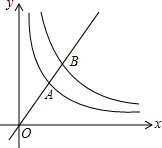 如图,在平面直角坐标系中,O为原点,直线y=kx(k>0)与双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)分别交于A,B两点,则$\frac{OB}{OA}$=$\sqrt{2}$.
如图,在平面直角坐标系中,O为原点,直线y=kx(k>0)与双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)分别交于A,B两点,则$\frac{OB}{OA}$=$\sqrt{2}$.
分析 根据直线y=kx(k>0)先设出A、B两点的坐标,作辅助线构建两个直角三角形,利用平行相似得比例式得出$\frac{OB}{OA}$等于A、B两点的纵坐标之比,由双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)计算出结论.
解答  解:设A(a,ka)、B(b,kb),
解:设A(a,ka)、B(b,kb),
分别过点A、B向x轴作垂线,垂足分别为C、D,
则AC∥BD,
∴△AOC∽△BOD,
∴$\frac{OB}{OA}$=$\frac{BD}{AC}$=$\frac{kb}{ka}$=$\frac{b}{a}$,
∵点A在双曲线y=$\frac{3}{x}$上,
∴ka2=3,k=$\frac{3}{{a}^{2}}$,
∵点B在双曲线y=$\frac{6}{x}$上,
∴kb2=6,k=$\frac{6}{{b}^{2}}$,
∴$\frac{3}{{a}^{2}}=\frac{6}{{b}^{2}}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=2,
∵A、B在第一象限,则a>0,b>0,
∴$\frac{b}{a}$=$\sqrt{2}$,
∴$\frac{OB}{OA}$=$\frac{b}{a}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了反比例函数与一次函数的交点,解此类题的思路为:先根据一个函数表示出交点的坐标,再利用另一个函数列方程或比例式求解,综合性较强.此题还通过作坐标轴的垂线构建相似三角形或全等三角形,利用它们的性质列式计算.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.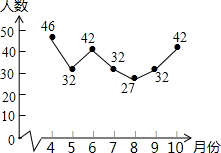 在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )
在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )
 在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )
在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )| A. | 46人 | B. | 42人 | C. | 32人 | D. | 27人 |
8.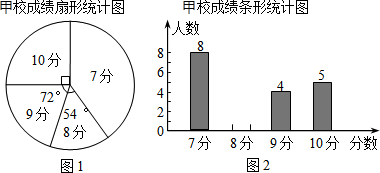 甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表
甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表
乙校成绩统计表
(1)在图1中,“7分”所在扇形的圆心角等于144度;
(2)请将图2的统计图和乙校成绩统计表补充完整;
(3)成绩最好的男同学王东、李亮.女同学张梅、萧红被选中参加电视辩论,辩论前抽签决定每两人为一组,请你用树状图和列表法表示所有可能的分组结果,并计算两名男同学恰好在同一组的概率.
 甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表
甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表乙校成绩统计表
| 分数 | 7分 | 8分 | 9分 | 10分 |
| 人数 | 11 | 0 | 8 |
(2)请将图2的统计图和乙校成绩统计表补充完整;
(3)成绩最好的男同学王东、李亮.女同学张梅、萧红被选中参加电视辩论,辩论前抽签决定每两人为一组,请你用树状图和列表法表示所有可能的分组结果,并计算两名男同学恰好在同一组的概率.
2.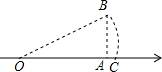 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以原点O为圆心,OB为半径画弧,交数轴于点C,则OC的长为( )
如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以原点O为圆心,OB为半径画弧,交数轴于点C,则OC的长为( )
 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以原点O为圆心,OB为半径画弧,交数轴于点C,则OC的长为( )
如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以原点O为圆心,OB为半径画弧,交数轴于点C,则OC的长为( )| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
6.下面计算正确的是( )
| A. | 6a-5a=1 | B. | a2+a2=2a4 | C. | -(a-b)=-a+b | D. | 2(a+b)=2a+b |