题目内容
10.按一定规律排列的一组数据:-$\frac{1}{2}$,$\frac{4}{3}$,-$\frac{9}{4}$,$\frac{16}{5}$,-$\frac{25}{6}$…,则第n个数据可表示为(-1)n$\frac{{n}^{2}}{n+1}$.分析 首先判断出每个数的正、负;然后根据2=1+1,3=2+1,4=3+1,5=4+1,判断出每个分数的分母等于这个数的项数加上1;最后根据1=12,4=22,9=32,16=42,…,判断出每个分数的分子等于这个数的项数的平方,据此求出第n个数据可表示为多少即可.
解答 解:因为这组数据分别是负数、正数、负数、正数、…,
所以每个数的正负等于-1的项数次方;
因为2=1+1,3=2+1,4=3+1,5=4+1,
所以每个分数的分母等于这个数的项数加上1;
又因为1=12,4=22,9=32,16=42,…,
所以每个分数的分子等于这个数的项数的平方,
所以第n个数据可表示为:(-1)n$\frac{{n}^{2}}{n+1}$.
故答案为:(-1)n$\frac{{n}^{2}}{n+1}$.
点评 此题主要考查了探寻数字规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:(1)每个数的正负等于-1的项数次方;(2)每个分数的分母等于这个数的项数加上1;(3)每个分数的分子等于这个数的项数的平方.

练习册系列答案
相关题目
5. 正方形ABCD的位置在坐标系中如图,点A、D的坐标分别为(1,0)、(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2015个正方形的面积为( )
正方形ABCD的位置在坐标系中如图,点A、D的坐标分别为(1,0)、(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2015个正方形的面积为( )
 正方形ABCD的位置在坐标系中如图,点A、D的坐标分别为(1,0)、(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2015个正方形的面积为( )
正方形ABCD的位置在坐标系中如图,点A、D的坐标分别为(1,0)、(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2015个正方形的面积为( )| A. | $5•{(\frac{3}{2})^{2013}}$ | B. | $5•{(\frac{3}{2})^{4026}}$ | C. | $5•{(\frac{3}{2})^{4028}}$ | D. | $5•{(\frac{3}{2})^{4030}}$ |
15.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x的值为( )
| A. | 0 | B. | ±1 | C. | 1 | D. | -1 |
20. 如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )
如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )
 如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )
如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )| A. | 10尺 | B. | 11尺 | C. | 12尺 | D. | 13尺 |
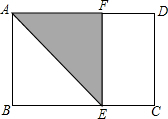 将长为1,宽为a的矩形纸片ABCD($\frac{1}{2}$<a<1)按如图方式折叠,剪下一个边长等于矩形宽度的正方形ABEF.若剩下的矩形EFDC与矩形ABCD相似,则a=$\frac{1+\sqrt{5}}{2}$.
将长为1,宽为a的矩形纸片ABCD($\frac{1}{2}$<a<1)按如图方式折叠,剪下一个边长等于矩形宽度的正方形ABEF.若剩下的矩形EFDC与矩形ABCD相似,则a=$\frac{1+\sqrt{5}}{2}$. 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.求:
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.求: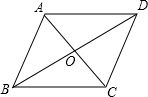 如图,平行四边形ABCD的对角线相交于O点,BC=14cm,BD=20cm,AC=12cm,则△AOD的周长为30cm.
如图,平行四边形ABCD的对角线相交于O点,BC=14cm,BD=20cm,AC=12cm,则△AOD的周长为30cm.