题目内容
5.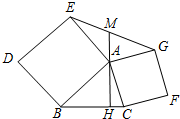 如图,以△ABC的边AB、AC为边向外作正方形ABDE和正方形ACFG,AH⊥BC,垂足为点H,交EG于点M.求证:EM=MG.
如图,以△ABC的边AB、AC为边向外作正方形ABDE和正方形ACFG,AH⊥BC,垂足为点H,交EG于点M.求证:EM=MG.
分析 利用“角角边”证明△ABH和△EAP全等,根据全等三角形对应边相等可得EP=AH,同理可证GQ=AH,从而得到EP=GQ,再利用“角角边”证明△EPM和△GQM全等,根据全等三角形对应边相等可得EM=MG.
解答 解:过点E作EP⊥HA的延长线于P,过点G作GQ⊥AM于Q,如图所示:
∵四边形ABDE是正方形,
∴AB=AE,∠BAE=90°,
∴∠EAP+∠BAH=180°-90°=90°,
∵AH⊥BC,
∴∠ABH+∠BAH=90°,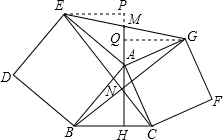
∴∠ABH=∠EAP,
在△ABH和△EAP中,
$\left\{\begin{array}{l}{∠ABH=∠EAP}&{\;}\\{∠AHB=∠P=90°}&{\;}\\{AB=AE}&{\;}\end{array}\right.$,
∴△ABH≌△EAP(AAS),
∴EP=AH,
同理可得:GQ=AH,
∴EP=GQ,
在△EPM和△GQM中,
$\left\{\begin{array}{l}{∠P=∠MQG}&{\;}\\{∠EMP=∠GMQ}&{\;}\\{EP=GQ}&{\;}\end{array}\right.$,
∴△EPM≌△GQM(AAS),
∴EM=MG.
点评 本题考查了正方形的性质、全等三角形的判定及性质的运用;通过作辅助线EP⊥HA的延长线于P,过点G作GQ⊥AM于Q构造出全等三角形是难点,运用全等三角形的性质是关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
6.下列说法错误的是( )
| A. | 平分弦的直径垂直于弦 | B. | 半圆(或直径)所对的圆周角是直角 | ||
| C. | 相等的圆心角所对的弧相等 | D. | 垂直半径的一端的直线是圆的切线 |
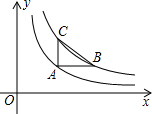 如图,已知点A在反比例函数y=$\frac{2}{x}$的图象上,点B,C分别在反比例函数y=$\frac{4}{x}$的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为(2,1).
如图,已知点A在反比例函数y=$\frac{2}{x}$的图象上,点B,C分别在反比例函数y=$\frac{4}{x}$的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为(2,1).


