题目内容
6. 如图,四边形ABCD是⊙O的内接四边形,延长DC,AB交于点E,且BE=BC.
如图,四边形ABCD是⊙O的内接四边形,延长DC,AB交于点E,且BE=BC.(1)求证:△ADE是等腰三角形;
(2)若∠D=90°,⊙O的半径为5,BC:DC=1:$\sqrt{2}$,求△CBE的周长.
分析 (1)根据圆内接四边形的性质和等腰三角形的判定定理证明;
(2)连接AC,设BC=k,根据等腰直角三角形的性质用k表示出AD、DC,根据勾股定理计算即可.
解答 (1)证明:∵四边形ABCD是⊙O的内接四边形,
∴∠A=∠BCE,
∵BE=BC,
∴∠BCE=∠BEC,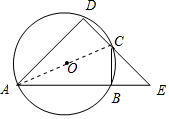 ∴∠A=∠BEC,
∴∠A=∠BEC,
∴DA=DE,即△ADE是等腰三角形;
(2)连接AC,
设BC=k,则CD=$\sqrt{2}$k,
∵∠D=90°,
∴∠CBE=∠D=90°,又BE=BC,
∴∠E=45°,
∴BE=BC=k,EC=$\sqrt{2}$k,
∴DE=2$\sqrt{2}$k,
由勾股定理得,AC=$\sqrt{10}$k,
∵⊙O的半径为5,
∴$\sqrt{10}$k=10,
解得,k=$\sqrt{10}$,
∴△CBE的周长为:2$\sqrt{10}$+2$\sqrt{5}$.
点评 本题考查的是圆内接四边形的性质、等腰直角三角形的性质,掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键,解答时,注意方程思想的灵活运用.

练习册系列答案
相关题目
18.已知分式方程$\frac{x}{x-2}$-$\frac{1}{{x}^{2}-4}$=1,去分母后得( )
| A. | x(x+2)-1=1 | B. | x(x-2)-1=x2-4 | C. | x(x+2)-1=x2-4 | D. | x-1=x2-4 |
15.把1米的线段进行黄金分割,则分成的较短的线段长为( )
| A. | $\frac{3-\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{1+\sqrt{5}}{2}$ | D. | $\frac{3+\sqrt{5}}{2}$ |
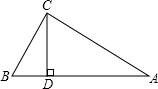 如图.在△ABC中,∠ACB=90°.CD是AB边上的高.∠A=30°.想一想:BD与AB有怎样的数量关系.
如图.在△ABC中,∠ACB=90°.CD是AB边上的高.∠A=30°.想一想:BD与AB有怎样的数量关系. 如图,D,E分别是AB,AC上的点,已知△AED∽△ABC,AD=4,BD=2,AC=8,求AE的长.
如图,D,E分别是AB,AC上的点,已知△AED∽△ABC,AD=4,BD=2,AC=8,求AE的长. 如图:在△ABC中,∠C=90°,点D是AB边上一点,DM⊥AB且DE=BC,过点M作ME∥BC交AB于点E.求证:ME=AB.
如图:在△ABC中,∠C=90°,点D是AB边上一点,DM⊥AB且DE=BC,过点M作ME∥BC交AB于点E.求证:ME=AB.