题目内容
10. 如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).
如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).(1)求△ABC的面积;
(2)若点A、C的位置不变,当点P在y轴上什么位置时,使S△ACP=2S△ABC?
分析 (1)根据点A、B、C的坐标求出AB,点C到AB的距离,然后根据三角形的面积公式列式计算即可得解;
(2)分点m>0和m<0两种情况,利用三角形的面积公式列式计算即可得解.
解答 解:(1)∵A(1,0),B(-2,3),C(-3,0),
∴AC=1-(-3)=1+3=4,
点B到AC的距离为3,
∴△ABC的面积=$\frac{1}{2}$×4×3=6;
(2)设P点的坐标(0,m),
∵S△ACP=2S△ABC,
∴$\frac{1}{2}×4$×|m|=2×$\frac{1}{2}$×4×3,
∴m=±6,
∴点P在y轴上坐标为(0,6)或(0,-6)时,△ABP的面积等于△ABC的一半.
点评 本题考查了坐标与图形性质,三角形的面积,观察图形确定出三角形的底边AB与底边上的高的长度是解题的关键.

练习册系列答案
相关题目
15.已知二次函数y=x2-6x+m的最小值是-3,那么m的值等于( )
| A. | 10 | B. | 4 | C. | 5 | D. | 6 |
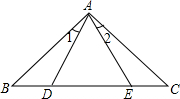 如图,AB=AC,∠1=∠2,AD=AE,则BD=CE.
如图,AB=AC,∠1=∠2,AD=AE,则BD=CE.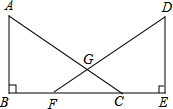 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:AB=DE.
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:AB=DE.