题目内容
11.小明、小颖和小凡做“石头、剪刀、布”游戏,游戏规则如下:由小明和小颖玩“石头、剪刀、布”游戏,如果两人的手势相同,那么小凡获胜;如果两人手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的获胜者.假设小明和小颖每次出这三种手势的可能性相同:(1)用树状图或列表法求出小凡获胜的概率;
(2)你认为这个游戏对三人公平吗?为什么?
分析 (1)列表得出所有等可能的情况数,找出两人手势相同的情况,求出小凡获胜的概率即可;
(2)找出小明与小颖获胜的情况数,求出两人获胜的概率,比较即可得到结果.
解答 解:(1)列出表格,如图所示:
| 石头 | 剪刀 | 布 | |
| 石头 | (石头,石头) | (剪刀,石头) | (布,石头) |
| 剪刀 | (石头,剪刀) | (剪刀,剪刀) | (布,剪刀) |
| 布 | (石头,布) | (剪刀,布) | (布,布) |
则P(小凡获胜)=$\frac{3}{9}$=$\frac{1}{3}$;
(2)小明获胜的情况有3种,小颖获胜的情况有3种,
∴P(小明获胜)=P(小颖获胜)=$\frac{3}{9}$=$\frac{1}{3}$,
则这个游戏对三人公平.
点评 此题考查了游戏公平性,以及列表法与树状图法,判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
相关题目
2.在下列实数$\frac{1}{4}$,$\sqrt{5}$,$-\sqrt{7}$,3.14,π.其中有理数出现的频率为( )
| A. | 20% | B. | 40% | C. | 60% | D. | 80% |
19.下列运算正确的是( )
| A. | a3+a3=a6 | B. | (a+b)2=a2+b2 | C. | (ab)2=a2b2 | D. | a6÷a3=a2 |
6.分式方程$\frac{1}{3x}$=$\frac{1}{2x}$+2的解为( )
| A. | x=$\frac{1}{2}$ | B. | x=$-\frac{1}{12}$ | C. | x=$\frac{1}{12}$ | D. | x=-12 |
16.关于二次函数y=x2-kx+k-1,以下结论:①抛物线交x轴有两个不同的交点;②不论k取何值,抛物线总是经过一个定点;③设抛物线交x轴于A、B两点,若AB=1,则k=4;④抛物线的顶点在y=-(x-1)2图象上;⑤抛物线交y轴于C点,若△ABC是等腰三角形,则k=-$\sqrt{2}$,0,1.其中正确的序号是( )
| A. | ①②⑤ | B. | ②③④ | C. | ①④⑤ | D. | ②④ |
20.下列说法正确的是( )
| A. | (3,2)和(2,3)表示同一个点 | B. | 点(1,0)在x轴的正半轴上 | ||
| C. | 点(-2,1)在第四象限 | D. | 点(-3,2)到x轴的距离为3 |
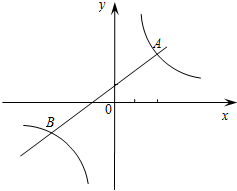 已知:如图,一次函数y=x+1与反比例函数$y=\frac{k}{x}$(k为常数,且k≠0)的图象相交于点A(2,m)、B两点.
已知:如图,一次函数y=x+1与反比例函数$y=\frac{k}{x}$(k为常数,且k≠0)的图象相交于点A(2,m)、B两点.