题目内容
1.抛物线y=x2+2x-3与x轴交点的坐标是(-3,0),(1,0).分析 令y=x2+2x-3=0,求出x的值,即可求出抛物线y=x2+2x-3与x轴交点的坐标.
解答 解:令y=x2+2x-3=0,
即(x+3)(x-1)=0,
解得x1=-3,x2=1,
所以抛物线y=x2+2x-3与x轴交点的坐标是(-3,0),(1,0),
故答案为(-3,0),(1,0).
点评 本题主要考查了抛物线与x轴交点的知识,正确把握抛物线与x轴交点个数确定方法是解题关键,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.化简:(-m)12÷(-m)3等于( )
| A. | m4 | B. | -m4 | C. | m9 | D. | -m9 |
10.在Rt△ABC中,∠C=90°,若斜边上的高为h,sinA=$\frac{3}{5}$,则AB的长等于( )
| A. | $\frac{5}{4}$h | B. | $\frac{5}{3}$h | C. | $\frac{25}{12}$h | D. | $\frac{12}{25}$h |
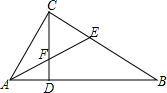 如图,△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC交CD于F,交BC于E,试说明△CEF是等腰三角形.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC交CD于F,交BC于E,试说明△CEF是等腰三角形.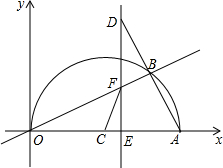 平面直角坐标系中,已知点A的坐标为(10,0),已知点C为中点,以c为圆心作圆,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.
平面直角坐标系中,已知点A的坐标为(10,0),已知点C为中点,以c为圆心作圆,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.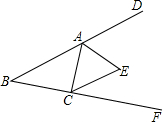 如图,在△ABC中,∠B=42°,△ABC的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=69°.
如图,在△ABC中,∠B=42°,△ABC的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=69°.