题目内容
在一个不透明的箱子里,装有2个红和2个黄球,它除了颜色外均相同.
(1)随机地从箱子里取出1个球,则取出红球的概率是多少?
(2)小明、小亮都想去观看足球比赛,但是只有一张门票,他们决定通过摸球游戏确定谁去.规则如下:随机地从该箱子里同时取出2个球,若两球颜色相同,小明去;若两球颜色不同,小亮去.这个游戏公平吗?请你用树状图或列表的方法,帮小明和小亮进行分析.
(1)随机地从箱子里取出1个球,则取出红球的概率是多少?
(2)小明、小亮都想去观看足球比赛,但是只有一张门票,他们决定通过摸球游戏确定谁去.规则如下:随机地从该箱子里同时取出2个球,若两球颜色相同,小明去;若两球颜色不同,小亮去.这个游戏公平吗?请你用树状图或列表的方法,帮小明和小亮进行分析.
考点:列表法与树状图法
专题:
分析:(1)直接利用概率公式求出即可;
(2)利用树状图法列举出所有的可能,进而利用概率公式求出即可.
(2)利用树状图法列举出所有的可能,进而利用概率公式求出即可.
解答:解:(1)∵在一个不透明的箱子里,装有2个红和2个黄球,它除了颜色外均相同,
∴随机地从箱子里取出1个球,取出红球的概率是:
=
;
(2)不公平,如图所示:

一共有12中情况,两球颜色相同的有4种情况,
故P(小明胜)=
,P(小亮胜)=
.
∴随机地从箱子里取出1个球,取出红球的概率是:
| 2 |
| 4 |
| 1 |
| 2 |
(2)不公平,如图所示:

一共有12中情况,两球颜色相同的有4种情况,
故P(小明胜)=
| 1 |
| 3 |
| 2 |
| 3 |
点评:此题主要考查了树状图法求概率,正确列举出所有可能是解题关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
规定一种运算符号”*”,且满足:a*b(a-b)2-1,如,3*2=(3-2)2-1=0,1*(-2)=[1-(-2)]2-1=8,那么,函数y=(2x)*2+2的最小值是( )
| A、1 | B、2 | C、3 | D、0 |
某小组为了解本校学生的视力情况,分别作了四种抽样调查的方案,你认为方案比较合理的是( )
| A、调查邻近学校200名学生的视力情况 |
| B、随机调查本校九年级50名学生的视力情况 |
| C、从每年级随机调查2个学生的视力情况 |
| D、随机调查本校各年级10%的学生视力情况 |
 如图,Rt△ABC中,CD是斜边AB上的高.求证:△ACD∽△ABC.
如图,Rt△ABC中,CD是斜边AB上的高.求证:△ACD∽△ABC.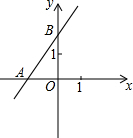 如图,直线y=2x+3与x轴交于点A,与y轴交于点B.
如图,直线y=2x+3与x轴交于点A,与y轴交于点B.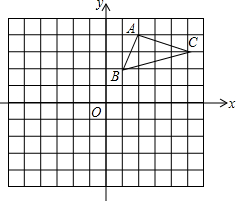 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题: