题目内容
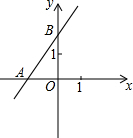 如图,直线y=2x+3与x轴交于点A,与y轴交于点B.
如图,直线y=2x+3与x轴交于点A,与y轴交于点B.(1)求三角形AOB的面积;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求BP的解析式.
考点:一次函数图象上点的坐标特征,待定系数法求一次函数解析式
专题:计算题
分析:(1)先根据坐标轴上点的坐标特征得到A(-
,0),B(3,0),然后根据三角形面积公式求解;
(2)分类讨论:当点P在点O的右侧,如图1,先确定P点坐标为(3,0),再利用待定系数法求直线PB的解析式;当点P在点O的左侧,如图2,先P点坐标为(-3,0),再利用待定系数法求直线PB的解析式.
| 3 |
| 2 |
(2)分类讨论:当点P在点O的右侧,如图1,先确定P点坐标为(3,0),再利用待定系数法求直线PB的解析式;当点P在点O的左侧,如图2,先P点坐标为(-3,0),再利用待定系数法求直线PB的解析式.
解答: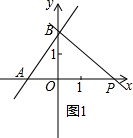 解:(1)当y=0时,2x+3=0,解得x=-
解:(1)当y=0时,2x+3=0,解得x=-
,则A点坐标为(-
,0);当x=0时,y=2x+3=3,则B点坐标为(3,0),
所以三角形AOB的面积=
×
×3=
;
(2)当点P在点O的右侧,如图1,
∵A点坐标为(-
,0),OP=2OA,
∴P点坐标为(3,0),
设直线PB的解析式为y=kx+b,则
,解得
,
∴直线PB的解析式为y=-x+3;
当点P在点O的左侧,如图2,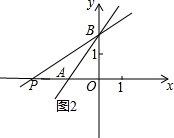
∵A点坐标为(-
,0),OP=2OA,
∴P点坐标为(-3,0),
设直线PB的解析式为y=kx+b,则
,解得
,
∴直线PB的解析式为y=x+3,
综上所述,直线BP的解析式为y=-x+3或y=x+3.
 解:(1)当y=0时,2x+3=0,解得x=-
解:(1)当y=0时,2x+3=0,解得x=-| 3 |
| 2 |
| 3 |
| 2 |
所以三角形AOB的面积=
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
(2)当点P在点O的右侧,如图1,
∵A点坐标为(-
| 3 |
| 2 |
∴P点坐标为(3,0),
设直线PB的解析式为y=kx+b,则
|
|
∴直线PB的解析式为y=-x+3;
当点P在点O的左侧,如图2,

∵A点坐标为(-
| 3 |
| 2 |
∴P点坐标为(-3,0),
设直线PB的解析式为y=kx+b,则
|
|
∴直线PB的解析式为y=x+3,
综上所述,直线BP的解析式为y=-x+3或y=x+3.
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-
,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.
| b |
| k |

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
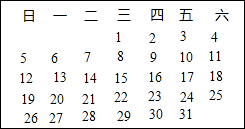 如图是2006年3月份的日历表,任意圈出一竖列上相邻的三个数,请你运用字母表示数来研究,这三个数的和不可能是( )
如图是2006年3月份的日历表,任意圈出一竖列上相邻的三个数,请你运用字母表示数来研究,这三个数的和不可能是( )| A、69 | B、54 | C、27 | D、40 |
下列几何体中,由两个面组成的是( )
| A、球 | B、圆锥 | C、圆柱 | D、三棱锥 |
下列说法中正确的是( )
| A、4的平方根是2 |
| B、-8没有立方根 |
| C、8的立方根是±2 |
| D、16的算术平方根是4 |

 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.