题目内容
18. 如图,已知△ABC中,∠ACB=90°,P是AC的中点.实践与操作:尺规作图:按下列要求完成作图
如图,已知△ABC中,∠ACB=90°,P是AC的中点.实践与操作:尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)
①以BC为直径作⊙O,交AB于点D;
②连接PD.推理与运用:求证:PD是⊙O的切线.
分析 ①如图所示,⊙O即为所求;
②连接OD、OC,首先证明∠3=∠4,∠1=∠2,由∠1+∠3=90°,即可推出∠4+∠2=90°;
解答 ①解:如图所示,⊙O即为所求.
②证明:连接OD、OC,
∵BC是直径,
∴∠BDC=90°,
∵点P是Rt△ADC斜边的中点,
∴PC=PA=PD,
∴∠3=∠4,
∵OC=OD,
∴∠1=∠2,
∵∠1+∠3=90°,
∴∠4+∠2=90°,
∴OD⊥PD,
∴PD是⊙O的切线.
点评 本题考查复杂作图,切线的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
2. 如图,已知直线AB、CD被直线AE所截,AB∥CD,∠1=60°,∠2的度数是( )
如图,已知直线AB、CD被直线AE所截,AB∥CD,∠1=60°,∠2的度数是( )
 如图,已知直线AB、CD被直线AE所截,AB∥CD,∠1=60°,∠2的度数是( )
如图,已知直线AB、CD被直线AE所截,AB∥CD,∠1=60°,∠2的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
 如图,有以下四个条件:①∠B+∠BCD=180°,②∠3=∠4,③∠1=∠2,④∠B=∠5.其中能判定AB∥CD的条件的有①③④ (填序号)
如图,有以下四个条件:①∠B+∠BCD=180°,②∠3=∠4,③∠1=∠2,④∠B=∠5.其中能判定AB∥CD的条件的有①③④ (填序号)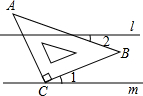 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为25度.
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为25度.