题目内容
19.若等腰三角形底边长为8cm,周长为36cm,则底角的正切值是$\frac{3\sqrt{5}}{2}$.分析 作等腰三角形底边上的高,将问题转化到直角三角形中,求底角的正切值即可.
解答  解:如图,∵BC=8,周长为36cm,
解:如图,∵BC=8,周长为36cm,
∴AB=AC=14,
过A点作AD⊥BC,垂足为D,
由等腰三角形的性质可知,BD=$\frac{1}{2}$BC=4,
在Rt△ABD中,由勾股定理,得AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{4}^{2}-{4}^{2}}$=6$\sqrt{5}$,
则tanB=$\frac{AD}{BD}$=$\frac{6\sqrt{5}}{4}$=$\frac{3\sqrt{5}}{2}$.
故答案为:$\frac{3\sqrt{5}}{2}$.
点评 本题考查了解直角三角,用到的知识点是锐角三角函数的定义及运用、勾股定理等腰三角形的性质,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
1.下面性质中菱形具有而平行四边形没有的性质是( )
| A. | 对角相等 | B. | 对角线互相平分 | C. | 对角线互相垂直 | D. | 对边平行 |
8.当a=$\frac{\sqrt{3}}{2}$,b=$\frac{3}{\sqrt{3}}$时,代数式ab+$\frac{a}{b}$的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
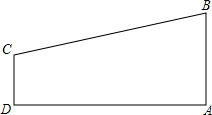 如图,在梯形ABCD中,AB∥DC,∠A=90°,AB=3,CD=2,AD=7,在AD上是否存在点P,使△ABP与△DCP相似?如果存在,求出DP的值;如果不存在,试说明理由.
如图,在梯形ABCD中,AB∥DC,∠A=90°,AB=3,CD=2,AD=7,在AD上是否存在点P,使△ABP与△DCP相似?如果存在,求出DP的值;如果不存在,试说明理由.