题目内容
14.化简或求值:(1)当a>0,b<0时,化简:$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|ab|}{ab}$;
(2)当1<x<2时,化简:$\frac{|x-2|}{x-2}$+$\frac{|x-1|}{x-1}$+$\frac{|x|}{x}$;
(3)当a+b+c=0,且ab>0,c<0时,设x=-|$\frac{|a|}{b+c}$+$\frac{|b|}{a+c}$+$\frac{|c|}{a+b}$|,求代数式x2015+2014x+2015的值.
分析 (1)利用绝对值的性质结合a,b的符号直接去绝对值得出答案;
(2)利用绝对值的性质结合x的取值范围,直接去绝对值得出答案;
(3)首先根据已知得出a>0,b>0,c<0,b+c=-a,a+c=-b,a+b=-c,进而代入求出x的值,即可得出答案.
解答 解:(1)当a>0,b<0时,
$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|ab|}{ab}$
=1-1-1
=-1;
(2)当1<x<2时,
$\frac{|x-2|}{x-2}$+$\frac{|x-1|}{x-1}$+$\frac{|x|}{x}$
=-1+1+1
=1;
(3)∵a+b+c=0,且ab>0,c<0,
∴a>0,b>0,c<0,b+c=-a,a+c=-b,a+b=-c,
∴x=-|$\frac{|a|}{b+c}$+$\frac{|b|}{a+c}$+$\frac{|c|}{a+b}$|
=-|$\frac{a}{-a}$+$\frac{b}{-b}$+$\frac{-c}{-c}$|
=-|-1-1+1|
=-1,
原式=x2015+2014x+2015
=(-1)2015+2014×(-1)+2015
=0.
点评 此题主要考查了代数式求值以及绝对值的性质,根据已知得出x的值是解题关键

练习册系列答案
相关题目
3.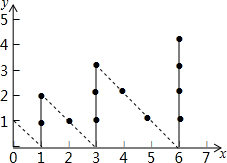 如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )
如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )
 如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )
如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )| A. | 886 | B. | 903 | C. | 946 | D. | 990 |
1.计算(-2a2)2÷2a的结果是( )
| A. | -2a2 | B. | 2a2 | C. | 2a3 | D. | -2a3 |
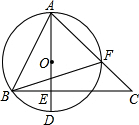 变式:如图,AD是⊙O的直径,AD⊥BC,△ABF与△ACB相似吗?
变式:如图,AD是⊙O的直径,AD⊥BC,△ABF与△ACB相似吗?