题目内容
3.如果关于x的方程(6-a)(9-a)x2-(117-15a)x+54=0的根都是整数,那么符合条件的整数a的值有几个?分析 分6-a=0、9-a=0和(6-a)(9-a)≠0三种情况考虑,当a=6或9时求出x的值,以此确定a=6或9是否合适;当(6-a)(9-a)≠0,利用分解因式法找出x1、x2的值,根据x1、x2以及a均为整数,找出a的值.综上即可得出结论.
解答 解:当6-a=0,即a=6时,原方程为-27x+54=0,
解得:x=2,
∴a=6合适;
当9-a=0,即a=9时,原方程为18x+54=0,
解得:x=-3,
∴a=9合适;
当(6-a)(9-a)≠0,即a≠6且a≠9时,(6-a)(9-a)x2-(117-15a)x+54=[(6-a)x-9][(9-a)x-6]=0,
∴x1=$\frac{9}{6-a}$,x2=$\frac{6}{9-a}$,
∵方程的根为整数,a为整数,
∴|6-a|=1、3、9且|9-a|=1、2、3、6,
解得:a=-3、3、5、7、15且a=3、7、8、10、11、12、15,
∴a=3、7、15.
综上:符合条件的整数a的值有5个.
点评 本题考查了因式分解法解方程,分6-a=0、9-a=0和(6-a)(9-a)≠0三种情况考虑是解题的关键.

练习册系列答案
相关题目
14. 已知,如图,点P关于OA、OB的对称点分别是P1,P2,分别交OA、OB于C,D,P1P2=6cm,则△PCD的周长为( )
已知,如图,点P关于OA、OB的对称点分别是P1,P2,分别交OA、OB于C,D,P1P2=6cm,则△PCD的周长为( )
 已知,如图,点P关于OA、OB的对称点分别是P1,P2,分别交OA、OB于C,D,P1P2=6cm,则△PCD的周长为( )
已知,如图,点P关于OA、OB的对称点分别是P1,P2,分别交OA、OB于C,D,P1P2=6cm,则△PCD的周长为( )| A. | 3cm | B. | 6cm | C. | 12cm | D. | 无法确定 |
15.下列命题中,是真命题的是( )
| A. | 如果a>b,则ac>bc | |
| B. | 直线外一点与直线上各点连接的所有线段中,垂线段最短 | |
| C. | 相等的角是对顶角 | |
| D. | 同旁内角互补 |
12.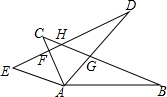 如图,AB=AD,AC=AE,∠BAD=∠CAE,现在有下列结论:①DE=BC;②AC⊥DE;③∠CAE=∠DHG;④S△ABG=S△AEF+S△DGH;⑤AF=AG,其中正确的结论个数为( )
如图,AB=AD,AC=AE,∠BAD=∠CAE,现在有下列结论:①DE=BC;②AC⊥DE;③∠CAE=∠DHG;④S△ABG=S△AEF+S△DGH;⑤AF=AG,其中正确的结论个数为( )
 如图,AB=AD,AC=AE,∠BAD=∠CAE,现在有下列结论:①DE=BC;②AC⊥DE;③∠CAE=∠DHG;④S△ABG=S△AEF+S△DGH;⑤AF=AG,其中正确的结论个数为( )
如图,AB=AD,AC=AE,∠BAD=∠CAE,现在有下列结论:①DE=BC;②AC⊥DE;③∠CAE=∠DHG;④S△ABG=S△AEF+S△DGH;⑤AF=AG,其中正确的结论个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13.超市出售的三种品牌月饼袋上,分别标有质量为(300±5)g,(300±10)g,(300±15)g的字样,从中任意拿出两袋,它们的质量最多相差( )
| A. | 10g | B. | 20g | C. | 30g | D. | 40g |
 如图,是长方形鸡场平面示意图,一边靠墙,并且墙长为18米,另外三面用竹篱笆围成,若竹篱笆总长为35m.
如图,是长方形鸡场平面示意图,一边靠墙,并且墙长为18米,另外三面用竹篱笆围成,若竹篱笆总长为35m. 我国古代的《河图》是由3×3的方格构成,每个方格均有数目不同的点图,每一行、每一列以及每一条对角线上的三个点图的点数之和均相等,如图给出了《河图》的部分点图,请你推算出P处所对应点图的点数是( )
我国古代的《河图》是由3×3的方格构成,每个方格均有数目不同的点图,每一行、每一列以及每一条对角线上的三个点图的点数之和均相等,如图给出了《河图》的部分点图,请你推算出P处所对应点图的点数是( )