题目内容
8.如图,把两个大小相同的含30°的直角三角形三角板的直角顶点叠合,其中一个三角形绕着直角顶点顺时针旋转”.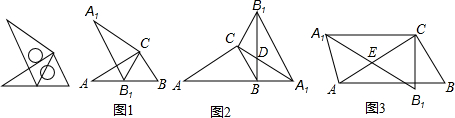
(1)图1是一种位置抽象出的几何图形,此时 A、B1、B在同一条直线上.如果AB=16厘米,则AB1的长为8厘米;
(2)图2也是一种位置抽象出的几何图形,此时A1在 AB的延长线上,试判断线段A A1和B B1的位置关系,并说明理由.
(3)在绕着直角顶点顺时针旋转过程中,设旋转角为a(0<a<90°),若A1B1交AC于E,联结A A1,若△A1EA是等腰三角形,请求出a的度数.
分析 (1)利用含30°的直角三角形的性质求出BC,再由旋转得出BC=B1C即可;
(2)先求出∠BCA1=30°,再得出∠CBB1=30°,即可得出∠ABB1=90°.
(3)分三种情况利用直角三角形性质和旋转的特征讨论计算
解答 解:两个大小相同的含30°的直角三角形三角板的直角顶点叠合,
∴AB=A1B1,BC=B1C1,AC=A1C1,∠BAC=∠B1A1C1=30°.
(1)Rt△ABC中,∠A=30°,
∴∠B=60°,BC=$\frac{1}{2}$AB=8cm,
由旋转知,BC=B1C,
∴△BCB1是等边三角形,
∴BB1=BC=8cm,
∴AB1=AB-BB1=8cm.
故答案为:8;
(2)在△CAA1中,CA=CA1,
∴∠CA1A=∠A=30°,
又∠CA1B1=30°,
∵∠ABC=∠AA1C+∠BCA1,
∴60°=30°+∠BCA1,∠BCA1=30°,
∴∠BCB1=120°,
又BC=B1C,
∴∠CBB1=$\frac{1}{2}$(180°-∠BCB1)=30°,
∴∠ABB1=90°,
即:AA1⊥BB1.
(3)△A1EA是等腰三角形,分三种情况:
①EA=EA1,则∠EA1A=∠EAA1,
∵CA=CA1,
∴∠CA1A=∠CAA1,
∴E、C重合,不合题意,舍去(C、E不可能重合).
②AA1=AE,∠A1AC=$\frac{1}{2}$(180°-α),
∴∠AA1E=∠AEA1=$\frac{1}{2}$[180°-$\frac{1}{2}$(180°-α)]=45°+$\frac{1}{4}$α,
又∠AA1E=∠AA1C-∠CA1B1=$\frac{1}{2}$(180°-α)-30°=60°-$\frac{1}{2}$α,
∴45°+$\frac{1}{4}$α=60°-$\frac{1}{2}$α,
∴α=20°,
③A1A=A1E,
则△A1AE∽△CAA1,
∠AA1E=α,∠A1EA=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α,
又∠A1EA=∠A1CA+∠CA1B1=α+30°,
∴90°-$\frac{1}{2}$α=α+30°,
∴α=40°.
综上所述,旋转角α=20°或40°.
点评 此题是几何变换综合题,主要考查了含30°的直角三角形的性质,旋转的性质,等腰三角形的性质,解本题的关键是寻找角之间的关系.

 阅读快车系列答案
阅读快车系列答案| A. | 10+1.8P | B. | 1.8P | C. | 10-1.8P | D. | 10+1.8(P-3) |
| A. | 所有的等腰三角形都是锐角三角形 | |
| B. | 等边三角形属于等腰三角形 | |
| C. | 不存在既是钝角三角形又是等腰三角形的三角形 | |
| D. | 一个三角形里有两个锐角,则一定是锐角三角形 |
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
| A. | 6 | B. | -6 | C. | $\frac{1}{6}$ | D. | -$\frac{1}{6}$ |
| A. | + | B. | - | C. | × | D. | ÷ |
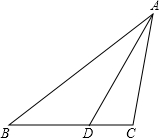 如图,在△ABC中,AC=BC,∠ACB=100°,AD是角平分线.求证:AB=AD+CD.
如图,在△ABC中,AC=BC,∠ACB=100°,AD是角平分线.求证:AB=AD+CD.